高考数学选修4-1几何题高考复习 29页

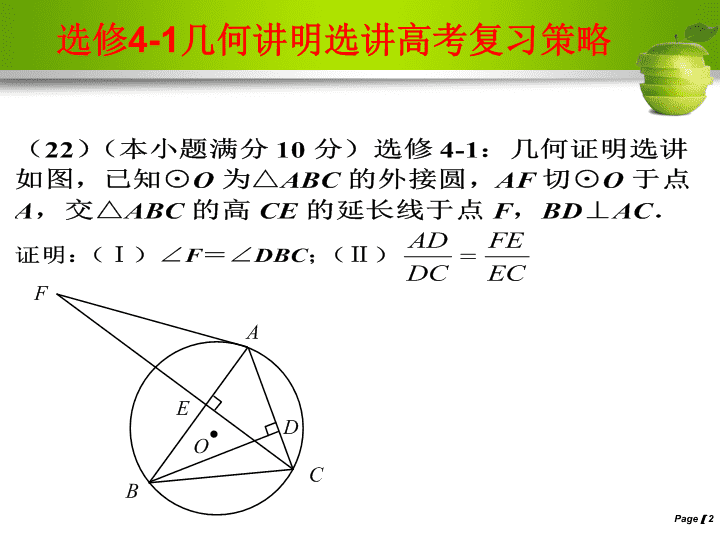
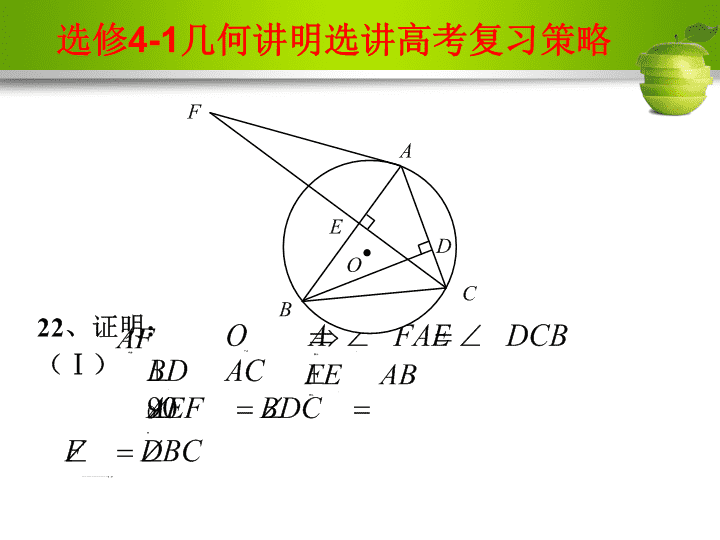
Page12012年高考数学选修4-1几何证明选讲备考复习昆明八中王学先\n选修4-1几何讲明选讲高考复习策略Page2\n选修4-1几何讲明选讲高考复习策略\nPage4\n选修4-1几何讲明选讲高考复习策略\n选修4-1几何讲明选讲高考复习策略\n选修4-1几何讲明选讲高考复习策略\n选修4-1几何讲明选讲高考复习策略((\n选修4-1几何讲明选讲高考复习策略((\n选修4-1几何讲明选讲高考复习策略\n选修4-1几何讲明选讲高考复习策略\n选修4-1几何讲明选讲高考复习策略\n选修4-1几何讲明选讲高考复习策略\n\n）AC）BD\n）AB）CD\n例。如图所示,已知⊙O1与⊙O2相交于A､B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1､⊙O2于点D､E,DE与AC相交于点P.(1)求证:AD∥EC;(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.\n\n类型四圆内接四边形的性质与判定解题准备:熟练运用圆内接四边形判定定理及其推论是证明四点共圆的关键,若证出四点共圆,便可运用圆内接四边形的性质解决相关问题.例如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.(1)证明:A,P,O,M四点共圆;(2)求∠OAM+∠APM的大小.[分析]要证A､P､O､M四点共圆,可考虑四边形APOM的对角互补;根据四点共圆,同弧所对的圆周角相等,进行等量代换,进而求出∠OAM+∠APM的大小.\n类型五弦切角与圆周角定理的应用解题准备:弦切角与圆周角是很重要的与圆相关的角.其主要功能在于协调与圆相关的各种角(如圆心角､圆周角等),是架设圆与三角形全等､三角形相似､与圆相关的各种直线(如弦､割线､切线)位置关系的桥梁,因而弦切角也是确定圆的重要几何定理的关键环节(如证明切割线定理).\n例如图所示,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证:ED2=EC·EB.[分析]利用弦切角定理､三角形内角平分线性质定理､切割线定理进行证明.\n类型六圆的切线的性质与判定解题准备:若知圆的切线,一种自然的想法就是连结过切点的半径,从而得到垂直关系.证明某条直线是圆的切线的常用方法有:若已知直线与圆有公共点,则需证明圆心与公共点的连线垂直于已知直线即可;若已知直线与圆没有明确的公共点,则需证明圆心到直线的距离等于圆的半径.\n例如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.[分析]因为DC过⊙O上的点D,所以可连接OD,只要证明DC⊥OD,因为BC和⊙O切于B,所以∠OBC=90°,因此只需证∠ODC=∠OBC,而这两个角分别在两个三角形中,只需证它们全等.\n类型六圆的切线的性质与判定解题准备:若知圆的切线,一种自然的想法就是连结过切点的半径,从而得到垂直关系.证明某条直线是圆的切线的常用方法有:若已知直线与圆有公共点,则需证明圆心与公共点的连线垂直于已知直线即可;若已知直线与圆没有明确的公共点,则需证明圆心到直线的距离等于圆的半径.\n选修4-1几何讲明选讲高考复习策略经验分享：1.利用平行线等分线段定理解题时要注意弄清题目所给的条件.常见的题型中，多与三角形的中位线、梯形的中位线相联系，因此取中点、作平行线是常用技巧.另外，要注意灵活运用三角形、平行四边形、等腰梯形的有关定理及性质.\n选修4-1几何讲明选讲高考复习策略2.相似三角形的性质把相似三角形的高、对应中线、对应角的平分线，以及周长、面积都与相似三角形的对应边的比(相似比)联系起来，利用相似三角形的性质可得到线段的比例、线段的平方比或角相等，有时还可用来计算三角形的面积、周长和边长.\n选修4-1几何讲明选讲高考复习策略3.运用射影定理时，要注意其成立的条件，要结合图形去记忆定理.当所给条件具备定理的条件时，可直接运用定理，有时也可通过作垂线使之满足定理的条件，再运用定理.在处理一些综合问题时，常常与三角形的相似相联系，要注意它们的综合运用.4.圆周(心)角定理及推论主要应用于证明弦相等或弧相等、角相等、垂直等.\n选修4-1几何讲明选讲高考复习策略\n谢谢！再见！