2020年秋人教版数学七年级期末复习专题 ：找规律之解答题专项（二） 15页

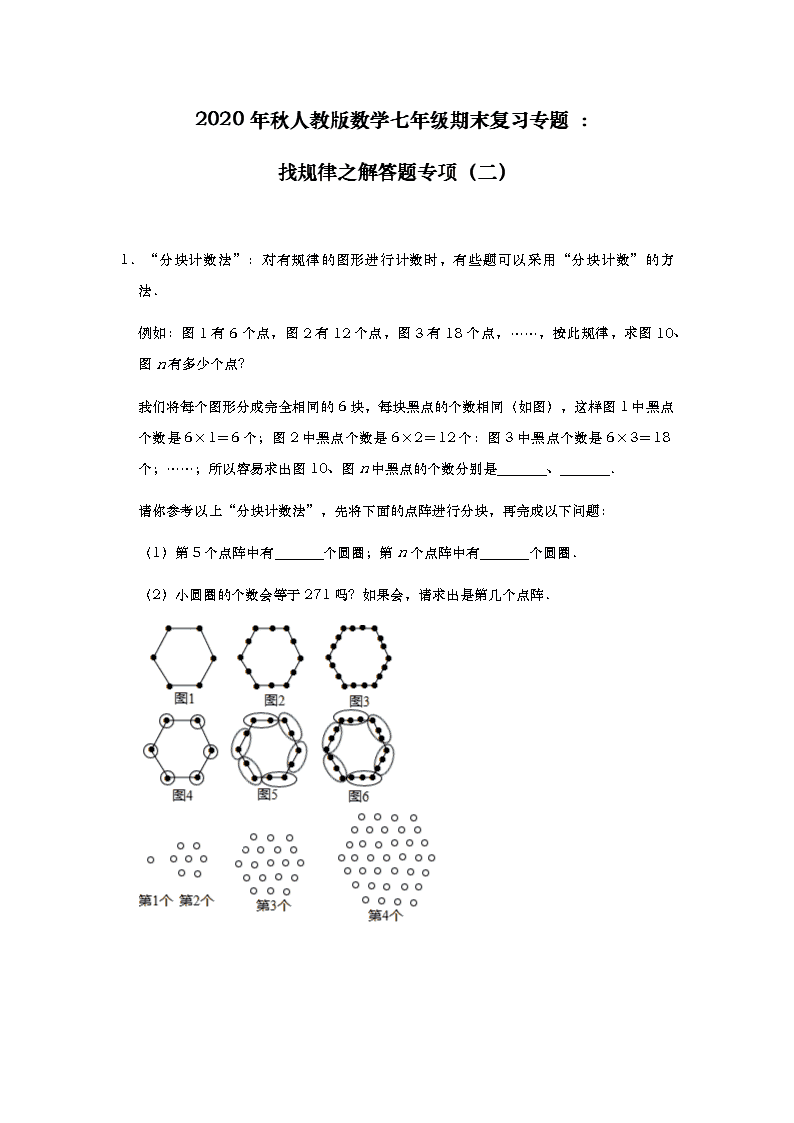
2020 年秋人教版数学七年级期末复习专题 ： 找规律之解答题专项（二） 1．“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法． 例如：图 1 有 6 个点，图 2 有 12 个点，图 3 有 18 个点，……，按此规律，求图 10、 图 n 有多少个点？ 我们将每个图形分成完全相同的 6 块，每块黑点的个数相同（如图），这样图 1 中黑点 个数是 6×1＝6 个；图 2 中黑点个数是 6×2＝12 个：图 3 中黑点个数是 6×3＝18 个；……；所以容易求出图 10、图 n 中黑点的个数分别是 、 ． 请你参考以上“分块计数法”，先将下面的点阵进行分块，再完成以下问题： （1）第 5 个点阵中有 个圆圈；第 n 个点阵中有 个圆圈． （2）小圆圈的个数会等于 271 吗？如果会，请求出是第几个点阵． 2．如图，图 1 中小黑点的个数记为 a1＝4，图 2 中小黑点的个数记为 a2＝8，图 3 中小黑 点的个数记为 a3＝13，… 根据以上图中的规律完成下列问题： （1）图 4 中小黑点的个数记为 a4，则 a4＝ ； （2）图 n 中小黑点的个数记为 an，则 an＝ （用含 n 的式子表示）； （3）第几个图形中的小黑点的个数为 43 个？ 3．观察下列图形与等式： ⇒ 22﹣12＝2×1+1×1； 图（1） ⇒ 32﹣22＝3×1+2×1； 图（2） ⇒ 42﹣32＝4×1+3×1； 图（3） ⇒ ？ 图（4） …… 根据图形面积与等式的关系找出规律，并结合其中的规律解决下列问题： （1）根据规律，图（4）对应的等式为 ； （2）请你猜想图（n）对应的等式（用含 n 的等式表示），并证明． 4．小明在学习第四章《基本平面图形》后，对一些规律性的问题进行了整理，请你在表格 中横线上填写正确的答案 1、线段问题 （例图） 线段上的点数 （包括 A、B） 线段数 （条） 3 3 4 6 … … 10 … … n 2、多边形对角线问题 （例图） 多边形 顶点个数 对角线 总条数 4 2 5 … … 10 … … n 3、角的问题 （例 图） ∠AOB 内增 加射线条数 角的总个数 1 3 2 … … 10 … n 5．用同样规格的黑，白两种颜色的正方形瓷砖按如图所示的方式铺宽为 1.5 米的小路 （1）铺第 5 个图形用黑色正方形瓷砖 块： （2）按照此方式铺下去，铺第 n 个图形用黑色正方形瓷砖 块：（用含 n 的代数 式表示） （3）若黑，白两种颜色的瓷砖规格都为（长为 0.5 米×宽 0.5 米），且黑色正方形瓷砖 每块价格 25 元，白色正方形瓷砖每块价格 30 元，若按照此方式铺满一段总面积为 18.75 平方米的小路时 n 是多少？该段小路所需瓷砖的总费用是多少？ 6 ． 用 黑 白 两 种 颜 色 的 正 六 边 形 地 砖 按 如 图 所 示 的 方 式 ， 拼 成 若 干 个 图 案 ： （1）当黑色地砖有 1 块时，白色地砖有 块，当黑色地砖有 2 块时，白色地砖有 块； （2）第 n（n 为正整数）个图案中，白色地砖有 块； （3）第几个图案中有 2018 块白色地砖？请说明理由． 7．归纳 人们通过长期观察发现，如果早晨天空中有棉絮状的高积云，那么午后常有雷雨降临， 于是有了“朝有破絮云，午后雷雨临”的谚语．在数学里，我们也常用这样的方法探求 规律，例如：三角形有 3 个顶点，如果在它的内部再画 n 个点，并以（n+3）个点为顶 点画三角形，那么最多以剪得多少个这样的三角形？ 为了解决这个问题，我们可以从 n＝1、n＝2、n＝3 等具体的、简单的情形入手，探索 最多可以剪得的三角形个数的变化规律． 三角形内点的个数 图形 最多剪出的小三角形个数 1 3 2 3 … … … （1）完成表格信息： 、 ； （2）通过观察、比较，可以发现： 三角形内的点每增加 1 个，最多可以剪得的三角形增加 个． 于是，我们可以猜想：当三角形内的点的个数为 n 时，最多可以剪得 个三角形． 像这样通过对现象的观察、分析，从特殊到一般地探索这类现象的规律、提出猜想的思 想方法称为归纳． 在日常生活中，人们互相交谈时，常常有人在列举了一些现象后，说“这（即列举的现 象）说明……”其实这就是运用了归纳的方法． 用归纳的方法得出的结论不一定正确，是否正确需要加以证实． （3）请你尝试用归纳的方法探索（用表格呈现，并加以证实）：1+3+5+7+…+（2n﹣ 1）的和是多少？ 8．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3， 5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和、现以这组数中 的各个数作为正方形的边长值构造如下正方形： 再分别依次从左到右取 2 个、3 个、4 个、5 个…正方形拼成如下长方形并记为①、②、 ③、④、…相应长方形的周长如下表所示： 序号 ① ② ③ ④ … 周长 6 10 x y … 仔细观察图形，上表中的 x＝ ，y＝ ． 若按此规律继续作长方形，则序号为⑧的长方形周长是 ． 9．如图，学校准备新建一个长度为 L 的读书长廊，并准备用若干块带有花纹和没有花纹的 两种规格大小相同的正方形地面砖搭配在一起，按图中所示的规律拼成图案铺满长廊， 已知每个小正方形地面砖的边长均为 0.3m． （1）按图示规律，第一图案的长度 L1＝ ；第二个图案的长度 L2＝ ； （2）请用代数式表示带有花纹的地面砖块数 n 与走廊的长度 Ln（m）之间的关系； （2）当走廊的长度 L 为 30.3m 时，请计算出所需带有花纹图案的瓷砖的块数． 10．阅读下面文字，解答题目中的问题． 阅读材料： ①平面上没有直线时，整个平面是 1 个区域； ②当平面上画出一条直线时，把平面分割成 2 个区域； ③当平面上有两条直线时，最多把平面分割成 4 个区域； ④当平面上有三条直线时，最多可以把平面分割成 7 个区域；… 解答下面问题： （1）根据上述事实填写下列表格： 平面上直线的条数 0 1 2 3 4 5 … 平面被分割成几个区 域 1 2 4 7 … （2）观察上表，猜想平面上有 n 条直线时，平面最多被分割成几个区域？（用含 n 的 代数式表示） （3）某校七年级（1）班 36 名同学为元旦联欢买来了一个特大蛋糕，如果要将这块蛋 糕分给每位同学，切 7 刀够吗？如果够，说明为什么；如果不够，至少要切几刀？ 参考答案 1．解：图 10 中黑点个数是 6×10＝60 个；图 n 中黑点个数是 6n 个， 故答案为：60 个，6n 个； （1）如图所示：第 1 个点阵中有：1 个， 第 2 个点阵中有：2×3+1＝7 个， 第 3 个点阵中有：3×6+1＝19 个， 第 4 个点阵中有：4×9+1＝37 个， 第 5 个点阵中有：5×12+1＝61 个， … 第 n 个点阵中有：n×3（n﹣1）+1＝3n2﹣3n+1， 故答案为：61，3n2﹣3n +1； （2）3n2﹣3n+1＝271， n2﹣n﹣90＝0， （n﹣10）（n+9）＝0， n1＝10，n2＝﹣9（舍）， ∴小圆圈的个数会等于 271，它是第 10 个点阵． 2．解：（1）根据题意知 a4＝1+2+3+4+5+4＝19， 故答案为：19； （2）an＝1+2+3+…+n+n+1+n ＝ +2n+1 ＝ n2+ n+1， 故答案为： n2+ n+1； （3）当 n2+ n+1＝43 时， 解得：n＝7 或﹣12（负值舍去）， 所以第 7 个图形中的小黑点的个数为 43 个． 3．解：观察上边图形面积与等式的关系： （1）图（4）对应的等式为： 52﹣42＝5×1+4×1， 故答案为：52﹣42＝5×1+4×1； （2）根据（1）发现规律： 图（n）对应的等式为： （n+1）2﹣n2═（n+1）×1+n×1 证明：左边＝n2+2n+1﹣n2＝2n+1， 右边＝2n+1， ∴左边＝右边， 即（n+1）2﹣n2＝（n+1）×1+n×1． 4．解：1、线段问题 线段上有 3 个点时，线段数为 1+2＝3 条； 线段上有 4 个点时，线段数为 1+2+3＝6 条； … 故当线段上有 10 个点时，线段数为 1+2+3+…+8+9＝（1+9）× ＝45 条； 当线段上有 n 个点时，线段数为 1+2+3+…+（n﹣1）＝（1+n﹣1）× ＝ 条； 填表如下： 2、多边形对角线问题 多边形有 4 个顶点时，对角线有 ＝2 条； 多边形有 5 个顶点时，对角线有 ＝5 条； 多边形有 10 个顶点时，对角线有 ＝35 条； 多边形有 n 个顶点时，对角线有 条； 填表如下： 3、角的问题 ∠AOB 内增加 1 条射线时，角的总数为：1+2＝3 条； ∠AOB 内增加 2 条射线时，角的总数为：1+2+3＝6 条； ∠AOB 内增加 10 条射线时，角的总数为：1+2+3+…+11＝ ＝66 条； ∠AOB 内增加 n 条射线时，角的总数为：1+2+3+…+（n+1）＝ 条． 填表如下： 5．解：（1）铺第 1 个图形用黑色正方形瓷砖的块数为 1×4+1＝5； 铺第 2 个图形用黑色正方形瓷砖的块数为 2×4+1＝9； 铺第 3 个图形用黑色正方形瓷砖的块数为 3×4+1＝13； … 铺第 5 个图形用黑色正方形瓷砖的块数为 5×4+1＝21； 故答案为 21； （2）根据（1）发现规律： 铺第 n 个图形用黑色正方形瓷砖的块数为（4n+1）； 故答案为（4n+1）； （3）根据题意，得 铺第 n 个图形用白色正方形瓷砖为 2（n+1）． ∴[（4n+1）+2（n+1）]×0.5×0.5＝18.75， 解得 n＝12． 该段小路所需瓷砖的总费用为： 25（4n+1）+30×2（n+1） 当 n＝12 时，160n+85＝2005． 答：该段小路所需瓷砖的总费用为 2005 元． 6．解：（1）当黑色地砖有 1 块时，白色地砖有 2+4＝6 块，当黑色地砖有 2 块时，白色 地砖有 2+4×2＝10 块， 故答案为：6、10； （2）根据题意知第 n（n 为正整数）个图案中，白色地砖有 2+4n（块）， 故答案为：4n+2． （3）令 4n+2＝2018， 解得：n＝504， 所以，第 504 个图案中有 2018 块白色地砖． 7．解；（1）由图形规律可得，答案为 5，7； （2）∵5﹣3＝7﹣5＝2， ∴三角形内的点每增加 1 个，最多可以剪得的三角形增加 2 个； ∵三角形内点的个数为 1 时，最多剪出的小三角形个数 3＝2×1+1， 三角形内点的个数为 2 时，最多剪出的小三角形个数 5＝2×2+1， 三角形内点的个数为 3 时，7 最多剪出的小三角形个数 7＝2×3+1， ∴三角形内点的个数为 n 时，最多剪出的小三角形个数 2n+1． 故答案为 2，（2n+1）； （3） 加数的个数 和 1+3 22 1+3+5 32 1+3+5+7 42 … … 1+3+5+7+…+（2n﹣ 1） n2 证明：∵S＝1+3+5+7+…+（2n﹣5）+（2n﹣3）+（2n﹣1） ∴S＝（2n﹣1）+（2n﹣3）+（2n﹣5）+…+7+5+3+1 ∴S+S＝2n•n＝2n2 2S＝2n2 S＝n2 8．解：由分析知：第 1 个长方形的周长为 6＝（1+2）×2； 第 2 个长方形的周长为 10＝（2+3）×2； 第 3 个长方形的周长为 16＝（3+5）×2； 第 4 个长方形的周长为 26＝（5+8）×2； 第 5 个长方形的周长为 42＝（8+13）×2； 第 6 个长方形的周长为 68＝（13+21）×2； 第 7 个长方形的周长为 110＝（21+34）×2； 第 8 个长方形的周长为 178＝（34+55）×2． 9．解：（1）第一图案的长度 L1＝0.3×3＝0.9，第二个图案的长度 L2＝0.3×5＝1.5； 故答案为：0.9，1.5； （2）观察可得：第 1 个图案中有花纹的地面砖有 1 块，第 2 个图案中有花纹的地面砖 有 2 块，… 故第 n 个图案中有花纹的地面砖有 n 块； 第一个图案边长 L＝3×0.3，第二个图案边长 L＝5×0.3，则第 n 个图案边长为 L＝ （2n+1）×0.3； （3）把 L＝30.3 代入 L＝（2n+1）×0.3 中得： 30.3＝（2n+1）×0.3， 解得：n＝50， 答：需要 50 个有花纹的图案． 10．解：（1）：①平面上没有直线时，整个平面是 1 个区域； ②当平面上画出一条直线时，把平面分割成 1+1＝2 个区域； ③当平面上有两条直线时，最多把平面分割成 1+1+2＝4 个区域； ④当平面上有三条直线时，最多可以把平面分割成 1+1+2+3＝7 个区域； ⑤当平面上有 4 条直线时，最多可以把平面分割成 1+1+2+3+4＝11 个区域； ⑥当平面上有 5 条直线时，最多可以把平面分割成 1+1+2+3+4+5＝16 个区域； 补全表格如下： 平面上直线的条数 0 1 2 3 4 5 … 平面被分割成几个区 域 1 2 4 7 11 16 … （2）当平面内有 n 条直线时，可以把一个平面最多分成 1+（1+2+3+…+n）＝1+ 个区域； （3）当切 7 刀的时候，最多可以切 1+ ＝29 个区域， 当切 8 刀的时候，最多可以切 1+ ＝37 个区域． ∴至少应切 8 刀．