福建省宁德市同心顺联盟2017_2018学年高一数学下学期期中试题 9页

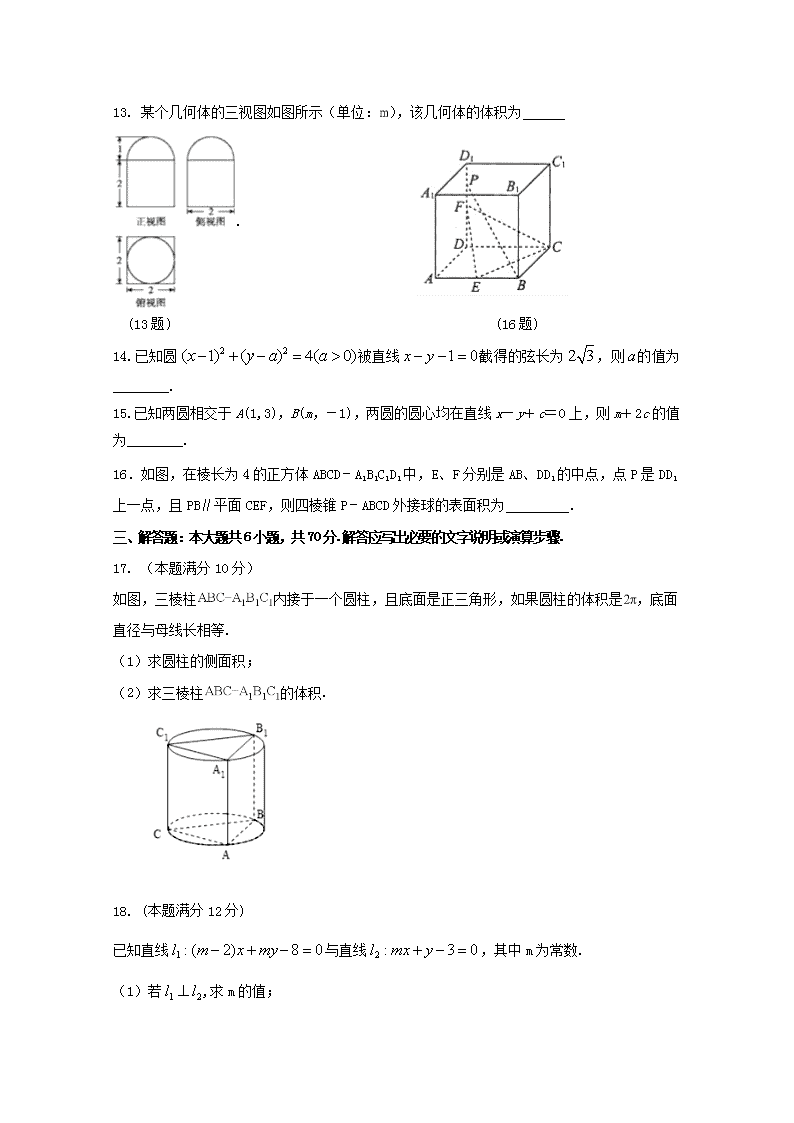
福建省宁德市同心顺联盟2017-2018学年高一数学下学期期中试题第I卷（选择题）和第II卷（非选择题）两部分，第I卷1至2页，第II卷3至4页。考试时间120分钟，满分150分。注意事项：　　1．答题前，考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名，考生要认真核对答题卡上粘贴的条形码的“准考证号，姓名”与考生本人准考证号、姓名是否一致。　　2．第I卷每小题选出答案后，用2B铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，第II卷用0.5毫米黑色签字笔在答题卡上书写作答，在试题卷上作答，答案无效。　　3．考试结束，考生必须将试题卷和答题卡一并交回。第I卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡的相应位置填涂．1.已知A（-1，3）、B（3，-1），则直线AB的倾斜角为A.45°B.60°C.120°D.135°2.直线，当变动时，所有直线恒过定点坐标为A.B.C.D.3．如图，一个水平放置的平面图形的斜二测直观图是一个底角为45ｏ，腰和上底均为1的等腰梯形，那么原平面图形的面积是A.B.C.D.4．若点P(－4，－2,3)关于坐标平面xOy及y轴的对称点的坐标分别是(a，b，c)，(e，f，d)，则c与e的和为A．1B．－1C．7D．－75.两圆x2＋y2－1＝0和x2＋y2－4x＋2y－4＝0的位置关系是A．内切B．相交C．外切D．外离6.在中，，，若把绕直线旋转一周，则所形成的几何体的体积为A．8B．C．16D．n7.已知平面，直线，且有，则下列四个命题正确的个数为①若∥则；②若∥则∥；③若则∥；④若则；A.B.C.D.8．如下图所示，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成四面体ABCD，则在四面体ABCD中，下列结论正确的是A．平面ABD⊥平面ABCB．平面ADC⊥平面BDCC．平面ABC⊥平面BDCD．平面ADC⊥平面ABC9.长方体中，，，分别是的中点，则异面直线与所成角为A.90°B.60°C.45D.30°10.某几何体的三视图如右图所示，则其侧面积为A．B．C．D．11.若圆C：x2＋y2－4x－4y－10＝0上至少有三个不同的点到直线l：x－y＋c＝0的距离为2，则c的取值范围是A．(－2,2)B．[－2,2]C．(－2，2)　　D．[－2，2]12.已知圆M：，直线，A为直线l上一点，若圆M上存在两点B，C，使得∠BAC=60°，则点A的横坐标的取值范围为A．[﹣1，1]B．[﹣4，2]C．[1，5]D．[2，6]第II卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分．请把答案填在答题卷的相应位置．n13.某个几何体的三视图如图所示（单位：），该几何体的体积为　　．(13题)(16题)14.已知圆被直线截得的弦长为，则的值为________.15.已知两圆相交于A(1,3)，B(m，－1)，两圆的圆心均在直线x－y＋c＝0上，则m＋2c的值为________.16．如图，在棱长为4的正方体ABCD﹣A1B1C1D1中，E、F分别是AB、DD1的中点，点P是DD1上一点，且PB∥平面CEF，则四棱锥P﹣ABCD外接球的表面积为　　　．三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或演算步骤.17.（本题满分10分）如图，三棱柱内接于一个圆柱，且底面是正三角形，如果圆柱的体积是，底面直径与母线长相等.（1）求圆柱的侧面积；（2）求三棱柱的体积.18.(本题满分12分)已知直线与直线，其中m为常数.（1）若,求m的值；n（2）若点P(1,2m)在上，直线过P点，且在两坐标轴上的截距之和为0，求直线的方程.19.(本题满分12分)如图，已知△ABC是正三角形，EA，CD都垂直于平面ABC，且EA＝AB＝2a，DC＝a，F是BE的中点，求证：(1)FD∥平面ABC；(2)AF⊥平面EDB.20.(本题满分12分)已知圆C：x2＋y2＋2x－4y＋1＝0，O为坐标原点，动点P在圆C外，过P作圆C的切线，设切点为M.(1)若点P的坐标为(1,3)，求此时切线l的方程；(2)求满足条件|PM|＝|PO|的点P的轨迹方程．21.(本题满分12分)如图，在底面是正方形的四棱锥面ABCD，BD交AC于点E，F、G分别是PC、AC上一点（1）求证：；（2）当二面角的大小为时，求PC与底面ABCD所成角的正切值.22.已知圆，点是直线上的一动点，过点作圆的切线，切点为.n(1)当切线的长度为时，求线段PM长度.(2)若的外接圆为圆，试问：当在直线上运动时，圆是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由；(3)求线段长度的最小值．n宁德市高中同心顺联盟2016-2017学年第二学期期中检测高一数学试题参考答案及评分标准一、选择题：本大题共12小题，每小题5分，共60分123456789101112DDBABCADACBC二、填空题：本大题共4小题，每小题5分，共20分．13．　　　14．15．116．41π三、解答题：本大题共6小题，共70分17．本题主要考查空间几何体的表面积和体积公式，考查空间想象能力、计算能力。满分10分。（1）设底面圆的直径为，由题可知...........................1∴…………………………….3∴圆柱的侧面积…………………………..........5（2）因为△ABC为正三角形，底面圆的半径为1，∴可得边长AB=.………………….....7∴三棱柱的体积.............................1018．本题主要考查直线的位置与系数的关系和求直线方程的方法，考查运算化简能力、数形结合思想、分类讨论思想。满分12分（1）∵∴............................2解得或................................4（2）若点P(1,2m)在上∴m=1,P为（1,2），…………………………..………...5∵直线l在两坐标轴上的截距之和为0当直线l过原点时，可设l的方程为，将点P（1,2）带入得∴此时l为;........................................................8当直线l不经过原点时，可设l的方程为，将点P（1,2）带入得∴此时l为……………………………………….....11n综上可得直线l的方程为或.........................1219．本题考查了直线与平面平行的判定，以及通过线线垂直推线面垂直。考查了空间想象能力，推理证明能力。满分12分。解：证明：(1)取AB的中点M，连接FM，MC.....……………………1∵F，M分别是BE，BA的中点，∴FM∥EA，FM＝EA＝a.......................2∵EA，CD都垂直于平面ABC，∴CD∥EA，∴CD∥FM......................................3又∵DC＝a，∴FM＝DC，∴四边形FMCD是平行四边形，............................4∴FD∥MC.∵FD⊄平面ABC，MC⊂平面ABC，∴FD∥平面ABC..................6(2)∵M是AB的中点，△ABC是正三角形，∴CM⊥AB...........................7又∵CM⊥AE，AB∩AE＝A，∴CM⊥平面EAB，∴CM⊥AF.........................................9又∵CM∥FD，∴FD⊥AF...................................................10∵F是BE的中点，EA＝AB，∴AF⊥BE...........................11又∵FD∩BE＝F，∴AF⊥平面EDB……………………………………….....1220.本题主要考查用点斜式求直线的方法，直线与圆相切的性质，直线与圆的位置关系，以及求轨迹方程的方法。考查了运算化简能力、数形结合思想、分类讨论思想。满分12分解：把圆C的方程化为标准方程为(x＋1)2＋(y－2)2＝4，∴圆心为C(－1,2)，半径r＝2.........................1(1)当l的斜率不存在时，此时l的方程为x＝1，C到l的距离d＝2＝r，满足条件．.....2当l的斜率存在时，设斜率为k，得l的方程为y－3＝k(x－1)，n即kx－y＋3－k＝0，..................................3则＝2，…………………………..4解得k＝－.................................5∴l的方程为y－3＝－(x－1)，即3x＋4y－15＝0综上，满足条件的切线l的方程为x＝1或3x＋4y－15＝0......6（2）设P(x，y)|PM|2＝|PC|2－|MC|2＝(x＋1)2＋(y－2)2－4，................8|PO|2＝x2＋y2，........................................10∵|PM|＝|PO|.∴(x＋1)2＋(y－2)2－4＝x2＋y2，整理，得2x－4y＋1＝0，∴点P的轨迹方程为2x－4y＋1＝0………………………...1221．本题主要考查了空间几何体的线面关系，二面角、直线与平面所成角，考查了空间想象能力，推理证明能力，化简运算能力。满分12分。解：（1）…………...1............................2........................................3..............................................4（2）作作于H，连接DH，，四边形ABCD是正方形，又是二面角的平面角，即.................6是PC与底面ABCD所成角………………………...7连接EH，则……………………………………...8又.........10，nPC与与底面ABCD所成角的正切值是....................................1222．本题主要考查的是直线和圆的位置关系，一般直线和圆的题很多情况下是利用数形结合来解决的，联立的时候较少；再者在求圆上的点到直线或者定点的距离时，一般是转化为圆心到直线或者圆心到定点的距离，再加减半径，分别得到最大值和最小值；圆的问题经常应用的性质有垂径定理的应用，切线长定理的应用.满分12分。（1）由题意知，圆M的半径r=4，圆心M(0，6)，设..............1PA是圆的一条切线，..........3(2)设，经过A,P,M三点的圆N以MP为直径，圆心，半径为..........................4得圆N的方程为即，有...........5由，解得或圆过定点..........7(3)圆N的方程，即①圆即②②-①得：圆M与圆N相交弦AB所在直线方程为：.....8圆心M(0,6)到直线AB的距离.............9弦长..................................11当时，线段AB长度有最小值....................................12