福建省莆田第一中学2019届高三数学下学期第四次月考试题文 9页

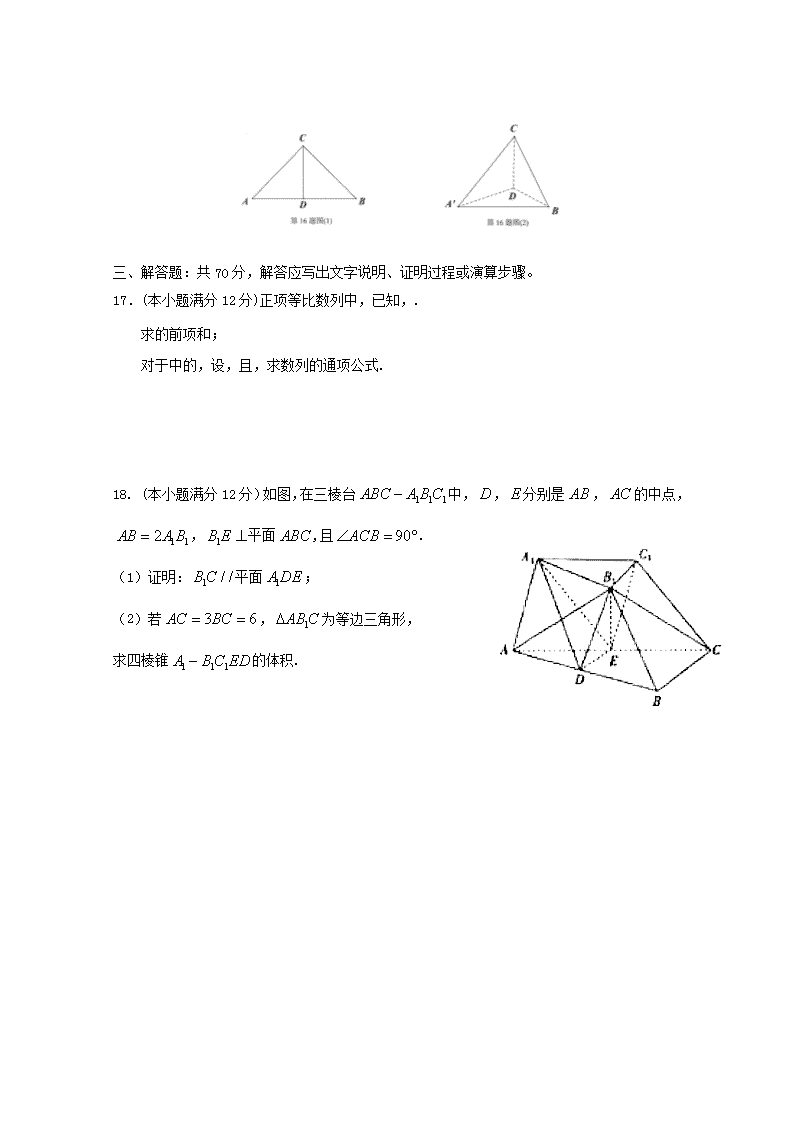
福建省莆田第一中学2019届高三数学下学期第四次月考试题文一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。1.已知全集，，，则（）A．B．C．D．2．已知i为虚数单位，复数满足，则在复平面上复数对应的点位于()A．第一象限B．第二象限C．第三象限D．第四象限3.将甲乙两个篮球队5场比赛的得分数据整理成如图所示的茎叶图，由图可知以下结论正确的是（）A.甲队平均得分高于乙队的平均得分B.甲队得分的中位数大于乙队得分的中位数C.甲队得分的方差大于乙队得分的方差D.甲乙两队得分的极差相等4.已知，则“”是“”的（）A．充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知双曲线的两条渐近线与圆相切于、两点且双曲线的右焦点与圆的圆心重合，则双曲线的实轴长为（）A.B.C.D.6．如图，大圆和小圆是同心圆，且曲边三角形关于圆心成中心对称.在该图案内取一点，则此点取自黑色部分的概率是（）A.B.C.D.7．函数的部分图象大致是（）8.《四元玉鉴》是中国古代数学的重要著作之一，由元代数学家朱世杰所著，创立四元消法，解多元高次方程组问题是该书的最大贡献，书中另两个重大成就是“垛积术”(高阶等差数列n求和）及“招差术”（有限差分），如图所示，程序框图的算法思路即源于该书的“茭草形段”问题，执行该程序框图，若输入的值是7，则输出的值为（）A.65B.140C.266D.4629.已知满足,则的取值范围是()A.B.C.D.（第8题）10.对于函数，下列说法正确的是（）A.在上单调递减B.有极小值C.有最小值D.有最大值11.在中，的对边分别为，若，，，则的值为（）A.B.C.D.12.若椭圆上存在三点，使得这三点与椭圆中心恰好是一个正方形的四个顶点，则该椭圆的离心率为（）A．B．C．D．二、填空题：本大题共4小题，每小题5分，共20分。13.已知向量,若,则.14.直线是曲线的切线，则实数=.15.已知均为锐角，且，则的最小值是.16.如图（1），在等腰直角ABC中，斜边AB=4，D为AB的中点，将ACD沿CD折叠得到如图（2）所示的三棱锥。若三棱锥的外接球的半径为，则=.n三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤。17．(本小题满分12分)正项等比数列中，已知，.求的前项和；对于中的，设，且，求数列的通项公式.18.(本小题满分12分）如图，在三棱台中，，分别是，的中点，，平面,且.（1）证明：平面；（2）若，为等边三角形，求四棱锥的体积.n19.(本小题满分12分）为积极响应国家“阳光体育运动”的号召，某学校在了解到学生的实际运动情况后，发起以“走出教室，走到操场，走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况，从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样，收集300位学生每周平均体育运动时间的样本数据(单位：小时)，得到如图所示的频率分布直方图。（已知高一年级共有1200名学生）（1）据图估计该校学生每周平均体育运动时间，并估计高一年级每周平均体育运动时间不足4小时的人数；（2）规定每周平均体育运动时间不少于6小时记为“优秀”，否则为“非优秀”，在样本数据中，有30位高三学生的每周平均体育运动时间不少于6小时，请完成下列列联表，并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”．基础年级高三合计优秀非优秀合计300P(K2≥k0)0.100.050.0100.005k02.7063.8416.6357.879附：K2＝20.(本小题满分12分）已知圆O：和一定点G（0，-6），过点G作圆O的两条切线GA，GB.（1）若G点关于原点的对称点为抛物线Q：的焦点，过P（1，0）且斜率为k的直线l与抛物线Q交于不同的两点M，N，，求实数k的值;（2）求与圆O外切，并且与直线GA,GB都相切的圆C的方程.n21.(本小题满分12分）设函数．若函数有两个不同的极值点，求实数的取值范围；若，，，且当时不等式恒成立，试求k的最大值．22．(本小题满分10分)选修4－4：坐标系与参数方程平面直角坐标系中，直线的参数方程为为参数，以原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为．写出直线的普通方程与曲线C的直角坐标方程；已知与直线平行的直线过点，且与曲线C交于A，B两点，试求．23.(本小题满分10分)选修4－5：不等式选讲已知函数．1)解不等式；若，求的取值范围．n莆田一中2018-2019学年度高三年级第四次月考试卷数学（文科）参考答案一、选择题：题　号123456789101112答　案BCCBDCBCABAD二、选择题：13.-114.115．16.三．解答题：17解：设正项等比数列的公比为，则由及得，化简得，解得或（舍去）.于是，所以，.由已知，，所以当时，由累加法得.又也适合上式，所以的通项公式为，.18.（1）证明：设与相交于，连接，由题意可知，，，所以四边形是平行四边形，--------------------2分从而是的中点.又是的中点，所以.----------------------4分又平面，平面，所以平面.----------------------6分（2）解：易证，是三楼柱，又因为平面，所以是此三棱柱的高，n同理也是三棱锥的高.----------------------8分因为，为等边三角形，所以，，,-----------------10分又，所以.--------------------12分19.（1）该校学生每周平均体育运动时间………3分样本中高一年级每周平均体育运动时间不足4小时的人数:又样本中高一的人数有120人，所以高一年级每周平均体育运动时间不足4小时的人数为1200=300………6分（2）列联表如下：基础年级高三合计优秀10530135非优秀10560165合计21090300………………8分假设该校学生的每周平均体育运动时间是否优秀与年级无关，则又.所以有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.12分20.解：（1）由题可得抛物线的方程为，设过P(1，0)且斜率为k的直线l的方程为n直线l与抛物线的交点为M()，N()，由得，，.-------------3分，即25,解得k=-25或1.又＞0或，或1。-------------6分（1）解法一：设圆C的半径为R，如图所示，由平面几何性质可得，（Ⅰ）当圆C在圆O的下方时，相似于，，解得R=1，圆C的方程为。-------------9分（Ⅱ）当圆C在圆O的上方时，相似于，，解得R=4，圆C的方程为，故所求圆C的方程为或。-------------12分解法二：由题可得切线GA，GB的方程为，，设圆C的方程为，-------------8分由题意知-------------10分解得或故所求圆C的方程为或。-------------12分21.(本小题满分12分）解：由题意知，函数的定义域为，，令，可得，，令，则由题可知直线与函数的图象有两个不同的交点，，令，得，可知在上单调递增，在上单调递减，，当x趋向于时，趋向于零，故实数a的取值范围为当时，，，即，因为，所以，令，n则，令，则，所以在上单调递增，，，故函数在上唯一的零点，即，故当时，，即，当时，，所以，所以，因为，所以，所以k的最大值为4．  22.解：把直线l的参数方程化为普通方程为．由，可得，曲线C的直角坐标方程为．直线l的倾斜角为，直线的倾斜角也为，又直线过点，直线线的参数方程为为参数，将其代入曲线C的直角坐标方程可得，设点A，B对应的参数分别为，．由一元二次方程的根与系数的关系知为，．．  23.解：；，故或或，解得：或，故不等式的解集是或；，，，，．