高考理科数学高考最新模拟试题 12页

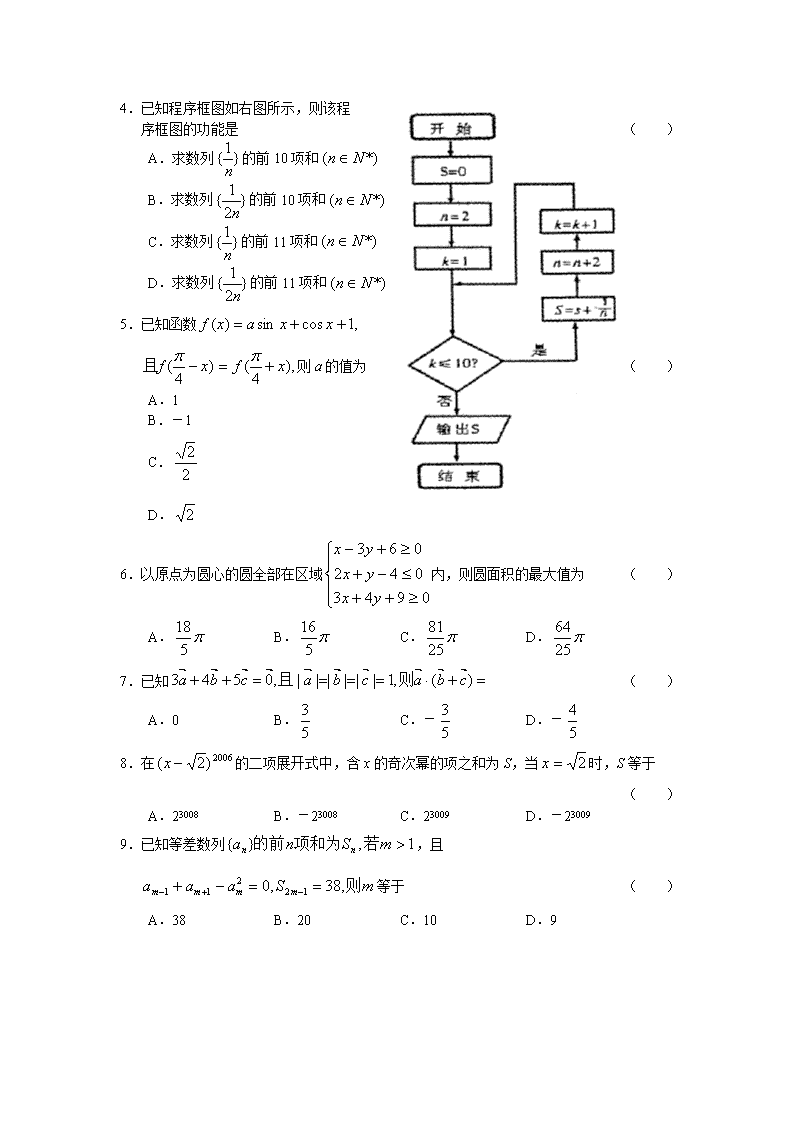
高考理科数学模拟试题本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分。满分100分，考试时间120分钟。考试结束后，将本试卷和答题卡一并交回。第Ⅰ卷（选择题，共50分）注意事项：1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡。2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。不能答在试题卷上。一、选择题（本卷有25道题，每小题2分，共50分。在每题列出的四个选项中，只有一项是最符合题目要求的。）参考公式：如果事件A、B互斥，那么正棱锥、圆锥的侧面积公式P（A+B）=P（A）+（B）如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）其中c表示底面周长，l表示斜高或母线长如果事件A在一次试验中发生的概率是球的体积公式P，那么n次独立重复试验中恰好发生k次的概率其中R表示球的半径一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，选择一个符合题目要求的选项。1．已知复数是实数，则实数b的值为（）A．0B．C．6D．－62．已知中心在原点，焦点在y轴的双曲线的渐近线方程为，则此双曲线的离心率为（）A．B．C．D．53．不等式成立的充分不必要条件是A．或B．C．或D．\n4．已知程序框图如右图所示，则该程序框图的功能是（）A．求数列的前10项和B．求数列的前10项和C．求数列的前11项和D．求数列的前11项和5．已知函数则a的值为（）A．1B．－1C．D．6．以原点为圆心的圆全部在区域内，则圆面积的最大值为（）A．B．C．D．7．已知（）A．0B．C．－D．－8．在的二项展开式中，含x的奇次幂的项之和为S，当时，S等于（）A．23008B．－23008C．23009D．－230099．已知等差数列，且等于（）A．38B．20C．10D．9\n2,4,610．已知是的零点，且，则实数a、b、m、n的大小关系是（）A．B．C．D．11．设O为坐标原点，F为抛物线的焦点，A为抛物线上的一点，若，则点A的坐标为（）A．（2，2）B．（1，±2）C．（1，2）D．（2，）12．正四面体ABCD的棱长为1，棱AB//平面，则正四面体上的所有点在平面内的射影构成图形面积的取值范围是（）A．B．C．D．2,4,6第Ⅱ卷（共90分）注意事项：1．用钢笔或圆珠笔直接答在试题卷中。2．答卷前将密封线内的项目填写清楚。二、填空题：本大题共4小题，每小题4分，共16分，答案须填在题中横线上。13．已知函数14．实数满足,则的最大值是15．对具有相同定义域的函数和，如果对任意有成立，则称和是上“密切函数对”.现给定义域均为，下列四对函数如下：\n①，；②，；③，；④，。其中是“密切函数对”番号是.16.设所有可表示为两整数的平方差的整数组成集合M.给出下列命题：①所有奇数都属于M.②若偶数2k及属于M，则.③若，则,,④把所有不属于M的正整数从小到大依次择成一个数列，则它的前n项和其中正确命题的序号是_______•(写出所有正确命题的序号》三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。17．（本小题满分12分）在△ABC中，已知角A、B、C所对的三条边分别是a、b、c，且（Ⅰ）求证：；（Ⅱ）求函数的值域。\n18.对任意都有（Ⅰ）求和的值．（Ⅱ）数列满足：=+，数列是等差数列吗？请给予证明；（Ⅲ）令试比较与的大小．19．（本小题满分12分）已知等腰梯形PDCB中（如图1），PB=3，DC=1，PD=BC=，A为PB边上一点，且PA=1，将△PAD沿AD折起，使面PAD⊥面ABCD（如图2）。（Ⅰ）证明：平面PAD⊥PCD；（Ⅱ）试在棱PB上确定一点M，使截面AMC把几何体分成的两部分；（Ⅲ）在M满足（Ⅱ）的情况下，判断直线AM是否平行面PCD.\na3a2a120．（本小题满分12分）某计算机程序每运行一次都随机出现一个五位的二进制数A=a5a4，其中A的各位数中，出现0的概率为，出现1的概率为.记，当程序运行一次时（I）求的概率；（II）求的分布列和数学期望.21．（本小题满分12分）已知抛物线的焦点为F，经过点F的直线l交抛物线于A、B两点，过A、B两点分别作抛物线的切线，设两切线的交点为M.（I）求点M的轨迹方程；（II）求证MF⊥AB.（III）设△MAB的面积为S，求S的最小值及此时直线l的方程.\n22．（本小题满分14分）设x=0是函数的一个极值点。（Ⅰ）求a与b的关系式（用a表示b），并求的单调区间；（Ⅱ）设，使得成立？若存在，求a的取值范围；若不存在，说明理由。\n参考答案一、选择题1．D2．B3．D4．B5．A6．B7．C8．B9．C10．A11．B12．D2,4,6二、填空题2,4,613．2/314．715．1,416．1,3三、解答题17．（本小题满分12分）解证：（I）由余弦定理得…………4分又…………6分（II）…………10分即函数的值域是…………12分18．（本小题满分12分）解：（Ⅰ）因为．所以．……2分令，得，即．……………4分（Ⅱ）又………………5分两式相加．所以，………………7分又．故数列是等差数列．………………9分（Ⅲ）\n………………10分………………11分所以……………………………………………………………………12分19．（本小题满分12分）（I）证明：依题意知：…………2分…4分（II）由（I）知平面ABCD∴平面PAB⊥平面ABCD.…………4分在PB上取一点M，作MN⊥AB，则MN⊥平面ABCD，设MN=h则…………6分要使即M为PB的中点.…………8分（III）以A为原点，AD、AB、AP所在直线为x，y，z轴，建立如图所示的空间直角坐标系则A（0，0，0），B（0，2，0），C（1，1，0），D（1，0，0），P（0，0，1），M（0，1，）由（I）知平面，则的法向量。…………10分又为等腰因为所以AM与平面PCD不平行.…………12分\n20．（本小题满分12分）解：（I）已知，只须后四位数字中出现2个0和2个1.…………4分（II）的取值可以是1，2，3，4，5，.…………8分的分布列是12345P…………10分…………12分（另解：记.）21．（本小题满分12分）解：（I）设M，由于是，分别过A、B两点的切线方程为①\n②…………2分解①②得③…………4分设直线l的方程为由④…………6分④代入③得即M故M的轨迹方程是…………7分（II）…………9分（III）的面积S最小，最小值是4…………11分此时，直线l的方程为y=1…………12分22．（本小题满分14分）解：（I）…………2分由…………4分\n当的单调增区间是，单调减区间是…………6分当的单调增区间是，单调减区间是…………8分（II）当上单调递增，因此…………10分上单调递减，所以值域是…………12分因为在…………13分所以，a只须满足解得即当、使得成立.…………14分