华师大版初中数学中考诊断考试 27页

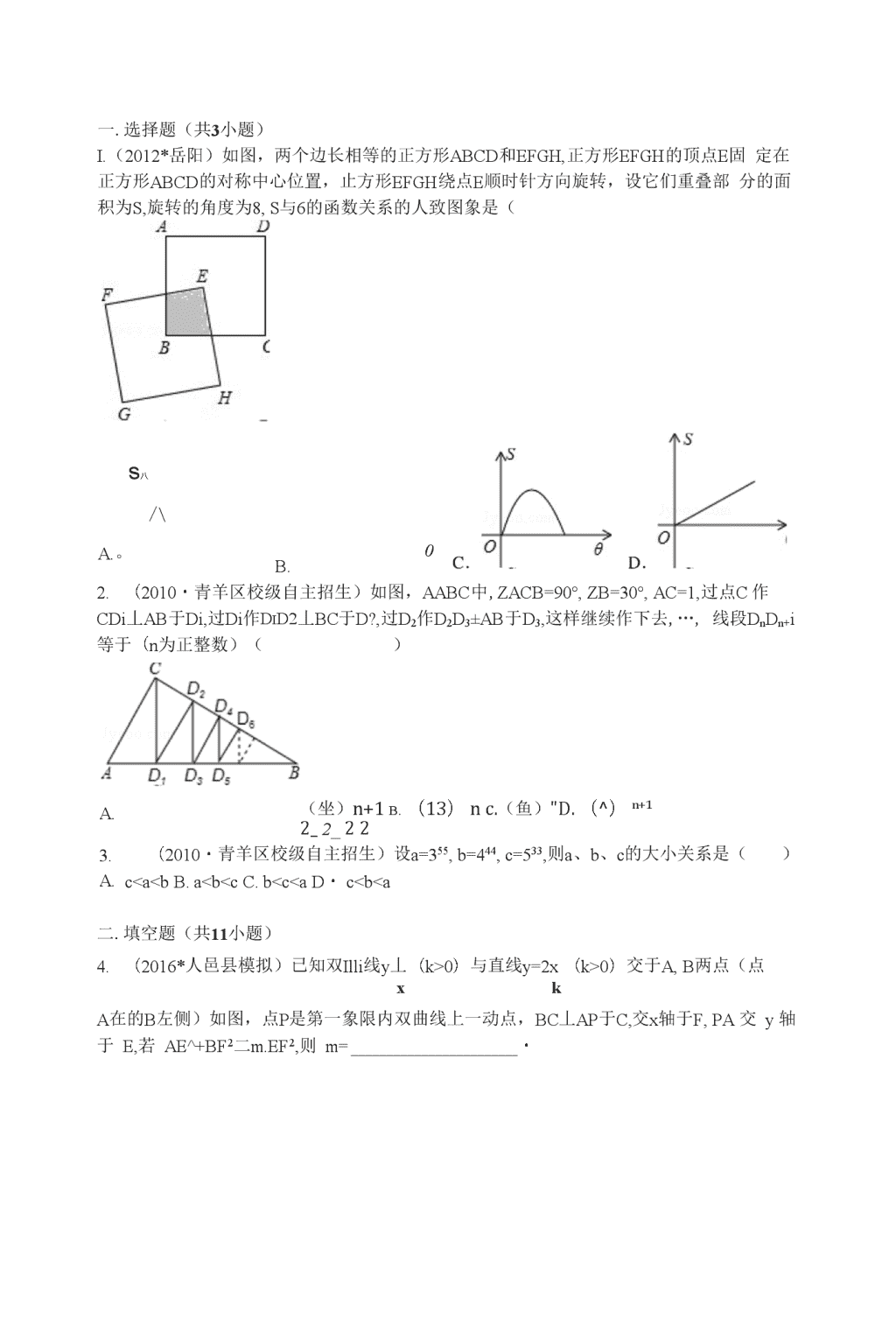
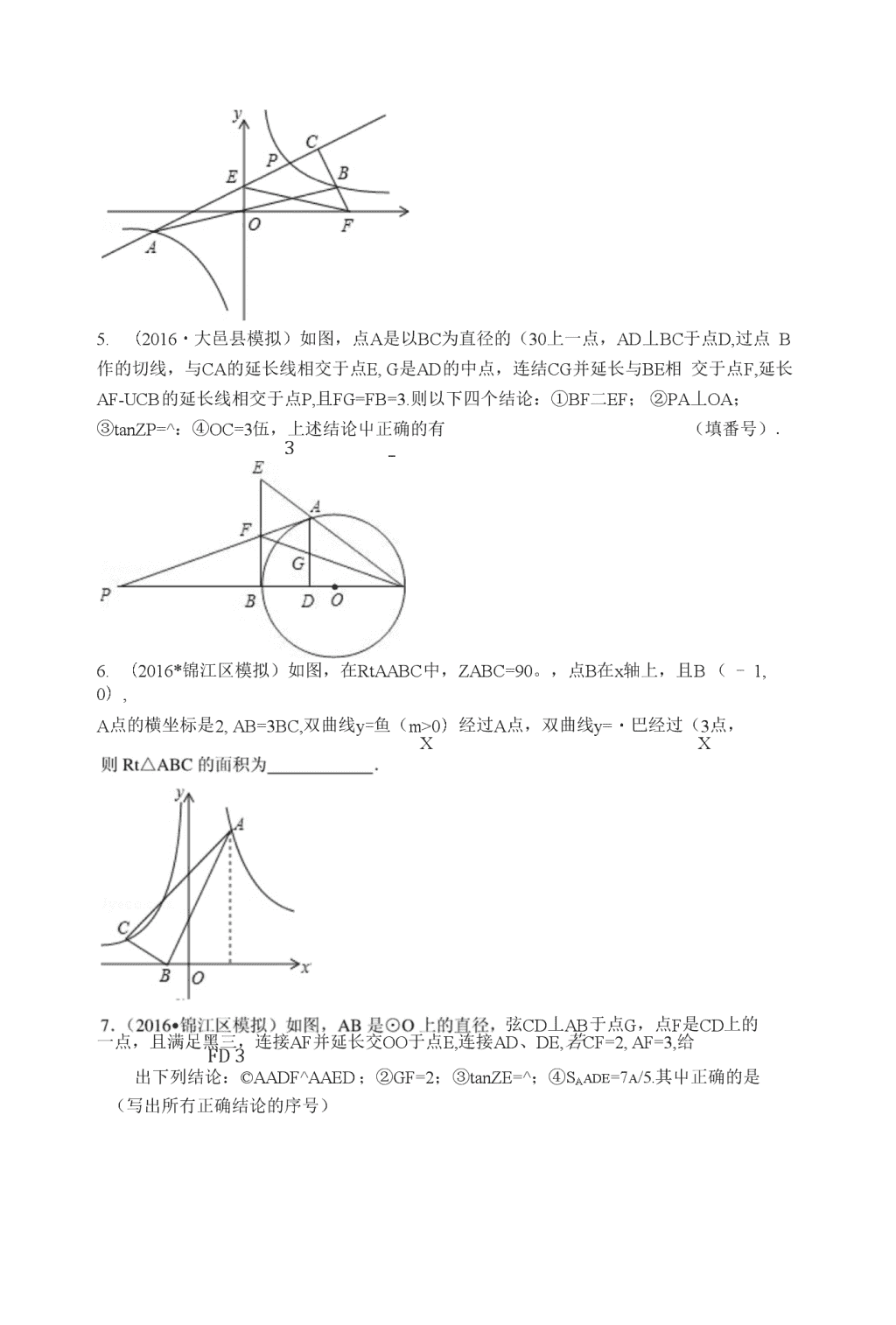
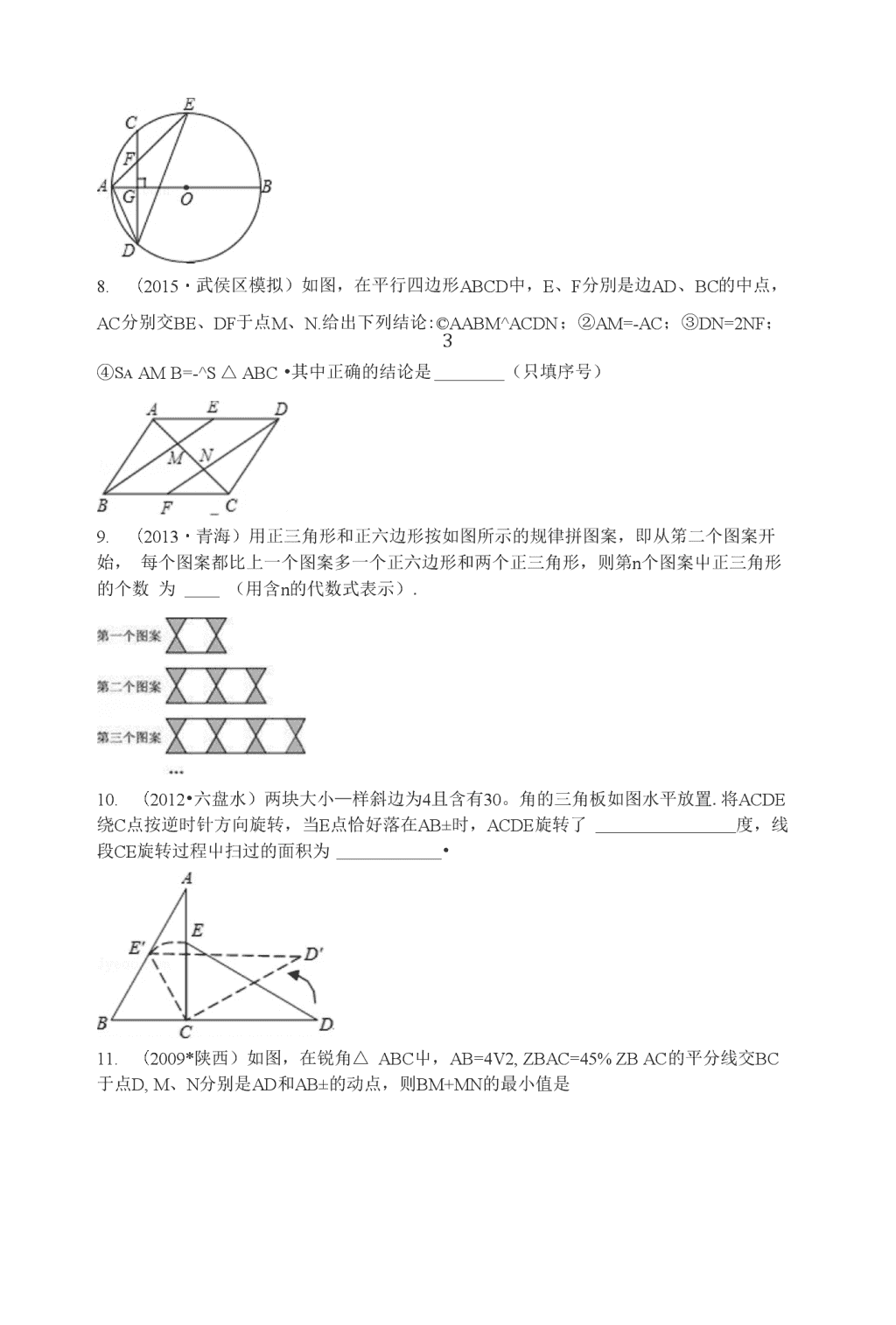
一.选择题（共3小题）I.（2012*岳阳）如图，两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，止方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S,旋转的角度为8,S与6的函数关系的人致图象是（s八/\A.。B.0A.3.A.2.（2010・青羊区校级自主招生）如图，AABC中,ZACB=90°,ZB=30°,AC=1,过点C作CDi丄AB于Di,过Di作DiD2丄BC于D?,过D2作D2D3±AB于D3,这样继续作下去,…,线段DnDn+i等于（n为正整数）（）（坐）n+1b.（13）nc.（鱼）"D.（^）n+12_2_22（2010・青羊区校级自主招生）设a=355,b=444,c=533,则a、b、c的大小关系是（）c0）与直线y=2x（k>0）交于A,B两点（点xkA在的B左侧）如图，点P是第一象限内双曲线上一动点，BC丄AP于C,交x轴于F,PA交y轴于E,若AE^+BF2二m.EF2,则m=・\n4.（2016・大邑县模拟）如图，点A是以BC为直径的（30上一点，AD丄BC于点D,过点B作的切线，与CA的延长线相交于点E,G是AD的中点，连结CG并延长与BE相交于点F,延长AF-UCB的延长线相交于点P,且FG=FB=3.则以下四个结论：①BF二EF；②PA丄OA；③tanZP=^：④OC=3伍，上述结论屮正确的有（填番号）.3_5.（2016*锦江区模拟）如图，在RtAABC中，ZABC=90。，点B在x轴上，且B（-1,0）,A点的横坐标是2,AB=3BC,双曲线y=鱼（m>0）经过A点，双曲线y=・巴经过（3点，XX弦CD丄AB于点G，点F是CD上的一点，且满足黑三，连接AF并延长交OO于点E,连接AD、DE,若CF=2,AF=3,给FD3出下列结论：©AADF^AAED；②GF=2；③tanZE=^；④SAade=7a/5.其屮正确的是（写出所冇正确结论的序号）\n8.（2015・武侯区模拟）如图，在平行四边形ABCD中，E、F分別是边AD、BC的中点，AC分别交BE、DF于点M、N.给出下列结论:©AABM^ACDN；②AM=-AC；③DN=2NF；3④SaAMB=-^S△ABC•其中正确的结论是（只填序号）9.（2013・青海）用正三角形和正六边形按如图所示的规律拼图案，即从笫二个图案开始，每个图案都比上一个图案多一个正六边形和两个正三角形，则第n个图案屮正三角形的个数为（用含n的代数式表示）.10.（2012•六盘水）两块大小—样斜边为4且含有30。角的三角板如图水平放置.将ACDE绕C点按逆时针方向旋转，当E点恰好落在AB±时，ACDE旋转了度，线段CE旋转过程屮扫过的面积为•11.（2009*陕西）如图，在锐角△ABC屮，AB=4V2,ZBAC=45%ZBAC的平分线交BC于点D,M、N分别是AD和AB±的动点，则BM+MN的最小值是\n8.（2012・黄石）“数学王子〃高斯从小就善于观察和思考.在他读小学吋就能在课堂上快速地计算出1+2+3+...+98+99+100=5050,今天我们可以将高斯的做法归纳如下：令S=l+2+3+...+98+99+100①S=100+99+98+...+3+2+1②①+②：冇2S=（1+100）xlOO解得：S=5050请类比以上做法，回答下列问题：若n为正整数，3+5+7+...+（2n+l）=168,则".9.（2005*绵阳）如图,在厶ABC中,BC=5cm,BP、CP分别是ZABC和ZACB的角平分线，且PD〃AB,PE〃AC,则APDE的周长是cm.10.（2010・青羊区校级自主招生）如图，正比例函数尸kx（k>0）与反比例函数尸卫的图x彖交于A、C两点，AB丄x轴于B,CD丄x轴于D,则S四边形abcd二•二.解答题（共16小题）11.（2016・人邑县模拟）“国美商场〃销售某品牌汤锅，其成本为每件80元，9月份的销售额为2万元，1（）月份商场对这种汤锅的售价打9折销售，结果销伟量增加了5（）件，销售额增加了0.7万元.（销售额二销售虽x售价）（1）求“国美商场〃9月份销售该品牌汤锅的销售单价；（2）11刀11日“购物节〃商场在9\n刀份售价的基础上打折促销（但不亏本），销售的数量y（件）与打折的折数x满足一次函数y=-50x4-600.问商场打几折时利润最人，最人利润是多少？（3）在（2）的条件下，为保证"国美商场〃利润不低于1.5万元，门能够最大限度帮助厂家减少库存，"国美〃商场应该在9月份销售价的基础上打几折？8.（2016•人邑县模拟）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形〃.（1）如图1,在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形〃.请写出你添加的一个条件.（2）小红猜想：对角线互相平分的“等邻边四边形〃是菱形•她的猜想正确吗？请说明理由.（3）如图2,小红作了一个RtAABC,其中ZABC=90°,AB=2,BC=1,并将RtAABC沿ZABC的平分线BBZ方向平移得到AA'B‘C',连结AA‘，BC'.小红要使得平移后的四边形ABC'A'是“等邻边四边形〃，应平移多少距离（即线段B‘B的长）？交x轴于A,B两点（A在B的左侧），过A点的直线y=kx+3k（k<--|）交c于另一点C（xi，yi）,交y轴于M.（1）求点A的坐标，并求二次函数的解析式；（2）过点B作BD丄AC交AC于D,若M（0,-3施）且Q点是肓线AC±的一个动点.求出当△DBQ-L/AAOM相似时点Q的坐标；（3）设P（・l,2）,图2中连CP交二次函数的图象于另一点E（x2,y2），连AE交y轴于N.OM・ON是否是一个定值？如果是定值，求出该值；若不是，请说明理由.18.（2016*锦江区模拟）已知，如图，AB是的直径，点C在OO±,过点C的直线与AB的延长线交于点P,ZCOB=2ZPCB,AC=PC.（1）求证：OC丄CP；（2）求cosZPAC的值；\n（3）点M是弧AB的中点，CM交AB于点N,若AB=6,求MN・MC的值.18.（2016*锦江区模拟）如图，己知线段AB,P是线段AB±任意一点（不与点A、B重合），分别以AP、BP为边，在AB的同侧作等边BPC,连接BD与PC交于点点E,连接CD.（备用图）..（1）当BC丄CD时，试求ZDBC的正切值；（2）若CD?=DE・DB,求证：DC=BE；（3）记四边形ABCD的而积为S,当P在线段AB±运动时，S与BD?是否成正比例？若成正比例，试求出比例系数；若不成正比例，试说明理由.19.（2016*锦江区模拟）己知如图1,二次函数y=ax2+4ax+^的图象交x轴于A、B两点（A4在B的左侧），过A点的直线y=kx+3k無>書）交该二次函数的图象于另一点C（xHyi）,交y轴于M.（1）直接写出A点坐标，并求该二次函数的解析式；（2）过点B作BD丄AC交AC于D,若M（0,3<3）且点Q是线段DC±的一个动点，求出当△DBQ与AAOM相似时点Q的坐标；（3）设P（・l,・2）,图2中连CP交二次函数的图彖于另一点E（X2，y2），连AE交y轴于N,请你探究OM・ON的值的变化情况，若变化，求其变化范围；若不变，求其值.\n18.（2015・武侯区模拟）如图，在平面直角坐标系中，点0是坐标原点，四边形ABCO是菱形，点A的坐标为（-3,4）,点C在x轴的正半轴上，直线AC交y轴于点M,AB边交y轴于点H.（1）求直线AC的函数关系式；（2）连接BM,动点P从点A岀发，沿折线A・B-C方向以2个单位/秒的速度向终点C匀速运动，设APIVIB的面积为S（ShO）,点P的运动时间为t秒，求S与tZ间的函数关系式（要求写出自变量t的取值范围）.19.（2015*武侯区模拟）如图（1）,ZABC=90°,O为射线BC上一点，OB=4,以点O为圆心，丄BO长为半径作交BC于点D、E.2（1）当射线BA绕点B顺时针方向旋转360。，若BA与OO相切时，那么BA旋转了多少度？（2）若射线BA绕点B按顺时针方向旋转与（DO相交于M、N两点（如图（2））,MN=2a/2,求五的反.20.（2015*武侯区模拟）已知如图，矩形OABC的长OA=V3,宽OC=1,将AAOC沿AC翻折得AAPC.（1）求ZPCB的度数；（2）若P,A两点在抛物线y=・|x2+bx+c±,求b,c的值，并说明点C在此抛物线上；（3）（2）中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点，N是y轴上的点，以点E、M、D、N为顶点的四边形是平行四边形，试求点M、N的坐标.\n18.(2()14・成都)如图,在00的内接△ABC中,ZACB=90°,AC=2BC,过C作AB的垂线1交OO于另一点D,垂足为E.设P是处上升于A,C的一个动点，射线AP交1于点F,连接PC与PD,PD交AB于点G.(1)求证：△PACsAPDF；(2)若AB=5,AP=BP,求PD的长；(3)在点P运动过程屮，设雪二x,tanZAFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)19.(2013・荆州)如图,已知：如图①,直线尸-VSx+VS与x轴、y轴分别交于A、B两点，两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止)；对称轴过点AH•顶点为M的抛物线y=a(x-k)2+h(a<0)始终经过点E,过E作EG〃0A交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分別是1个单位长度/秒和逅个单位长度/秒，运动时间为t秒.(1)用含I代数式分别表示BF、EF、AF的长;(2)当t为何值时，四边形ADEF是菱形？判断此时AGB是否和似，并说明理由；(3)当AADF是直角三角形，且抛物线的顶点M恰好在BG±时，求抛物线的解析式.\n图①图②18.（2005*常徳）如图，AB是OO的直径，BC是OO的弦，OO的割线PDE垂直AB丁•点F,交BC于点G,连接PC,ZBAC=ZBCP,求解下列问题：（1）求证：CP是OO的切线.（2）当ZABC=30°,BG=2V3,CG=4、/3时，求以PD、PE的长为两根的一元二次方程.（3）若（1）的条件不变，当点C在劣弧AD±运动时，应再具备什么条件可使结论bg2=bf*bO成立？试写出你的猜想，并说明理由.19.（2010・青羊区校级自主招生）已知：抛物线尸/-（a+b）x+y,其中a、b、c是AABC的ZA、ZB、ZC的对边.（1）求证：抛物线与x轴必有两个不同交点；（2）设直线y=ax-be与抛物线交于E、F两点，与y轴交于点M,抛物线与y轴交于点N,若抛物线的对称轴为x二a,AMNE与AlVINF的而积比为5：1,求证：AABC是等边三角形；（3）在（2）的条件下，设AABC的面积为逅，抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆？若存在，求出圆的圆心处标，若不存在，请说明理由.\n18.（2014*武侯区校级自主招生）数独（sudoku）是一种源自18世纪末的瑞士，后在美国发展、并在口木发扬光人的数学智力拼图游戏.拼图是九宫格（即3格宽x3格高）的正方形状，每-•格乂细分为一个九宫格.在每一个小九宫格中，分别填上1至9的数字，让整个大九宫格每一列、每一行的数字都不重复.下面是一个数独游戏，请完成该游戏.（您只需要完整地填出其屮的5个小九宫格即可）（评分标准：完整地填出其中的5个小九宫格且5个均正确即可给满分.未填出5个不给分.若填出超过5个且无错给满分，若填出超过5个且有任何一•处错误不给分.）235198674652247197327656455132j446219.（2005*资阳）如图,已知O为坐标原点,ZAOB=3（）°,ZABO=9（）°,且点A的坐标为（2,0）.（1）求点B的坐标；（2）若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的解析式；（3）在（2）中的二次两数图象的OB段（不包括点O、B）上，是否存在一点C,使得四边形ABCO的面积最人？若存在，求出这个最人值及此时点C的坐标；若不存在，请说明20.（2005*武汉）已知：如图，岂线尸-号x+3交x轴于Oi，交y轴于02,g与x轴相切于O点，交直线502于P点，以Oi为圆心，OiP为半径的圆交x轴于A、B两点，PB交002于点F,OO］的弦BE=BO,EF的延长线交AB于D,连接PA、PO.（1）求证：ZAPO=ZBPO；\n(2)求证：EF是002的切线；(3)EOi的延长线交0Oi于C点，若G为BC±一动点，以OiG为直径作003交O1C于点M,交0]B于N.下列结论：①O]M・O]N为定值；②线段MN的长度不变.只有一个是正确的，请你判断出正确的结论，并证明正确的结论，以及求出它的值.\n参考答案与试题解析一.选择题（共3小题）1.（2012・岳阳）如图，两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S,旋转的角度为3S与8的函数关系的人致图象是（）B.C.【分析】过点E作EM丄BC于点M,EN丄ABJ*点N,则可证HJ]AENK^AEML,从而得出重叠部分的面积不变，继而可得岀函数关系图象.2.（2010・青羊区校级自主招生）如图,AABC中，ZACB=90°,ZB=30°,AC=1,过点C作CDi丄AB于Di,过Di作DiD2丄BC于D?,过D2作D2D3±AB于D3,这样继续作下去，…,线段DnDn+i等于（n为正整数）（）A.（坐）n+1b.（13）nC.（鱼）nD.（^）n+12_2_22【分析】根据30。的直角三处形中，较长的直角边与斜边的比为逅：2,前面一个三角形较长的直角边是后面一个三角形的斜边，由此得出--般规律.2.（2010・青羊区校级自主招生）设a=355,b=444,c=533,则a、b、c的大小关系是（）A.c0）与直线y=—x（k>0）交于A,B两点（点xkA在的B左侧）如图，点P是第一象限内双曲线上一动点，BC丄AP于C,交x轴于F,PA交y轴于E,若AE^+BF2二nzEF2,则m=1.【分析】先求出A、B两点坐标，设点P（a,虫），求出直线AP、BC得E、F两点坐标,a利用两点间距离公式列出方程即可解决.3.（2016・大邑县模拟）如图，点A是以BC为直径的OO±一点，AD丄BC于点D,过点B作<30的切线，与CA的延长线相交于点E,G是AD的屮点，连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论：①BF二EF；②PA丄0A；③tanZP=^l：④0C=3近,上述结论中正确的冇①②④（填帝号）.3_墙即可证明.②正确，只要证明ZFAB+ZOAB=90。即可.③错误，求出AH,FH,根据咙PWnZAFH需诺晋,即可解决问题.④正确，在RTAAD0中利用勾股定理即可求出半径.4.（2016*锦江区模拟）如图,在RtAABC中，ZABC=90°,点B在x轴上,且BC1,0）,A点的横坐标是2,AB=3BC,双曲线y=—（m>0）经过A点，双曲线XX则RtAABC的而积为—・—2—\n过点C作CF丄x轴于F,由A点的横坐标是2,且在双曲线y=鱼（m>0）上，求出点的坐标，得到线段的长度，利用三角形相似得到点的坐标,x列方程求解.2.（2016・锦江区模拟）如图，AB是OO上的直径，弦CD丄AB于点G,点F是CD±的一点，且满足空二丄，连接AF并延长交。0于点E,连接AD、DE,若CF=2,AF=3,给FD3出下列结论：①△ADFs/XAED；②GF=2；③tanZE=^；④Smde=7运.其中正确的是2①②④（写岀所有正确结论的序号）【分析】①由AB是OO的直径，弓玄CD丄AB,根据垂径定理可得：AD=AC,DG=CG,继而证得△ADF^AAED；①由空=丄，CF=2,可求得DF的长，继而求得CG=DG=4,则可求得FG=2；FD3②由勾股定理可求得AG的长，即可求得tanZADF的值，继而求得tanZE=^；£③首先求得AADF的而积，由相似三角形而积的比等于相似比的平方，即可求得AADE的面积.3.（2015・武侯区模拟）如图，在平行四边形ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于点M、N.给出下列结论:①△ABM^ACDN；②AM=2ac；③DN=2NF；3®S/\amb=-^S/\abc-其中正确的结论是①②③（只填序巧）\nAE【分析】关键是证明四边形BFDE是平行四边形nBE〃DF,就可以利用平行线等分线段定理或利用和似推出其他结论了.2.（2013*青海）用正三角形和正八-边形按如图所示的规律拼图案，即从第二个图案开始，侮个图案都比上一个图案多一个正六边形和两个正三角形，则第n个图案中正三角形的个数【分析】对于找规律的题冃首先应找出哪些部分发生了变化，是按照什么规律变化的.3.（2012•六盘水）两块大小--样斜边为4且含有30。角的三角板如图水平放宜・将ACDE绕（2点按逆时针方向旋转，当E点恰好落在AB上时，ACDE旋转了30度,线段CE旋转过程中扫过的面积为―亏―【分析】根据含冇30。角的直角三角形的性质可知CE'是AACB的中线，可得AE'CB是等边三角形，从而得岀ZACE'的度数和CE'的长，从而得出ACDE旋转的度数；再根据扇形面积公式计算求解.4.（2009*陕西）如图,在锐角△ABC中,AB=4V2,ZBAC=45°,ZBAC的平分线交BC于点D,M、N分別是AD和AB.I：的动点，则BM+MN的最小值是一4.ANB\n【分析】从已知条件结合图形认真思考，通过构造全等三角形，利用三介形的三边的关系确定线段和的最小值.2.(2012・黄石)“数学王子〃高斯从小就善于观察和思考.在他读小学时就能在课堂上快速地计算出1+2+3+...+98+99+100=5050,今天我们可以将高斯的做法归纳如下:令S=l+2+3+...+98+99+100S=1()0+99+98+...+3+2+1①+②：有2S=(1+100)xlOO解得：S=5050请类比以上做法，回答卜-列问题：若n为正整数，3+5+7+...+(2n+l)=168,贝ijn=12.【分析】根据题目提供的信息，列出方程，然后求解即可.3.(2005・绵阳)如图，在ZXABC中，BC=5cm,BP、CP分别是ZABC和ZACB的角平分线，且PD〃AB,PE〃AC,则APDE的周长是5cm.【分析】分别利用角平分线的性质和平行线的判定，求得ADBP和AECP为等腰三角形，山等腰三角形的性质得BD=PD,CE=PE,那么APDE的周长就转化为BC边的长，即为5cm.4.(2()1()・青羊区校级自主招生)如图，正比例函数y二kx(k>0)与反比例函数尸卫的图X象交于A、C两点，AB丄x轴于B,CD丄x轴于D,则S四边形ABCD=6.【分析】先根据正比例函数y=x与反比例y=」的图彖均关于原点对称可知A、C两点关于原x点对称，故厶OAB与厶OBC同底等高，故其面积相等，同理可知AAOD与ACOD的面积也和等，再根据反比例函数系数k的几何意义即nJ求IIIAAOBAiACOD的面积，进而可求出答案.三.解答题（共16小题）\n2.（2016・人邑县模拟）〃国美商场〃销伟某品牌汤锅，其成本为每件80元，9月份的销伟额为2万元，10月份商场对这种汤锅的售价打9折销售，结果销售量增加了50件，销售额增加了0.7万元.（销售额=销售量X售价）（1）求“国美商场〃9月份销售该品牌汤锅的销售单价；（2）11月11日“购物节〃商场在9月份传价的基础上打折促销（但不亏本），销售的数量y（件）为打折的折数x满足一次函数y=-50x+600.问商场打几折时利润最大，最大利润是多少？（3）在（2）的条件下，为保证"国美商场〃利润不低于1.5万元，且能够最人限度帮助厂家减少库存，"国美〃商场应该在9月份销售价的基础上打几折？【分析】（1）根据人民商场销售某保温水瓶，其成本为每件80元，9刀份的销售额为2万元，10月份商场对这种保温瓶的售价打9折销售，结果销售量增加了50件，销售额增加了0.7万元，可以设出9刀份的保温瓶销售单价和销售数量，从而nJ以列出相应的二元一次方程组，即可解答本题；（2）根据题意可以列出销售利润的关系式，将其化为顶点式，即可求得最大利润和此吋的打折数；（3）由（2）和题意可以列出相应的关系式，从而可以求得x的范围，结合题意取舍即可.3.（2016*人邑县模拟）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形〃・（1）如图1,在四边形ABCD中，添加一个条件使得四边形ABCD是"等邻边四边形〃.请写出你添加的一个条件.（2）小红猜想：対角线互和平分的"等邻边四边形〃是菱形.她的猎想正确吗？请说明理山.（3）如图2,小红作了一个RtAABC,其中ZABC=90°,AB=2,BC=1,并将RtAABC沿ZABC的平分线BB'方向平移得到AA'B'C',连结AA‘,BC'・小红要使得平移后的四边形ABC'A'是“等邻边四边形〃，应平移多少距离（即线段B‘B的长）？【分析】（1）利用“等邻边四边形〃的定义直接判断即可，（2）利用平行四边形的判定和“等邻边四边形〃的定义直接判断即可，（3）利用“等邻边四迦刃的定义和平移的性质（对应线段平行且相等），分四种情况（AA‘=AB,AA‘=2C1,A'C/=BC/,BC‘=AB）进行讨论计算即可・4.（2016・大邑县模拟）图1中，二次函数y=-ax2-4ax-的图象c交x轴于A,B两点（人在站勺左侧），过A点的肓•线尸kx+3k（k<~交c于另一点C（xi，yi）,交y轴于M.（1）求点A的处标，并求二次函数的解析式；（2）过点B作BD丄AC交AC于D,若M（0,-3逅）且Q点是玄线AC上的一个动点.求\n出当与AAOM相似时点Q的坐标；（3）设P（・l,2）,图2中连CP交二次函数的图象于另一点E（x2,y2），连AE交y轴于N.OM・ON是否是一个定值？如果是定值，求出该值；若不是，请说明理由.【分析】（1）由直线y=kx+3k求出点A坐标，代入抛物线解析式即可解决问题.（2）分四种情形讨论①如图1中，当Q在DA的延长线上时,ZBQD=30°,ABQD〜△AOM,②当Q与点A重合时，ZBQD=60°ADQB〜△OAM,③如图2中，当Q在线段DC±时,ZBQD=60。，ADQB-AOAM,④如图3屮，当ZBQD=30°时，△DQB〜AOMA分别解宜角三角形即可.（3）求出直线PC的解析式，与抛物线组成方程组求出点E处标，再求出直线AE后求出点N坐标，用k表示OM、ON即可解决问题.2.（2016*锦江区模拟）已知，如图，AB是OO的直径，点C在0O±,过点C的直线与AB的延长线交于点P,ZCOB=2ZPCB,AC=PC・（1）求证:OC丄CP；（2）求cosZPAC的值；（3）点M是弧AB的中点，CM交AB于点N,若AB=6,求MN・MC的值.【分析】（1）已知C在圆上，故只需证明OC与PC垂直即可；根据圆周角定理，易得ZPCB+ZOCB=90°,即OC丄CP；（2）AB是直径；故只需证明BC与半径相等即可；继而求得cosZPAC的值；（3）连接MA,MB,市圆周角定理可得ZACM=ZBCM,进而可得△MBNs^MCB,故BM2=MN*MC；又由AABM是等腰氏角三角形，即可求得BM的值，继而求得答案.3.（2016*锦江区模拟）如图，已知线段AB,P是线段AB±任意一点（不少点A、B重合），分别以AP、BP为边，在AB的同侧作等边AAPD和ABPC,连接BD与PC交于点点E,连接CD.\nDPB（备用图）APB（1）当BC丄CD时，试求ZDBC的正切值；（2）若CdJdE・DB,求证：DC=BE；（3）记四边形ABCD的面积为S,当P在线段AB±运动时，S与BD?是否成正比例？若成正比例，试求出比例系数；若不成」E比例，试说明理由.【分析】（1）根据等边三角形的性质得出PC=BC,ZCPD=60°,PD〃BC,进而得岀ZDBC的正切值等于黒皐，即可得出答案;BCPC（3）由AD〃PC'PD〃BC，得出麴囁莎黑，进而得出孕二SABPC氏SAPDC%PDC^ABPC（2）利用线段CD是线段DE和DB的比例中项得JllADCE^ADBC,再利用相似三角形的性质得出即可;以及二申,即可得出比例系数.BD242.（2016*锦江区模拟）CM如图1,二次函数y=ax2+4ax+-?的图象交x轴于A、B两点（A在B的左侧），过A点的直线y=kx+3k鉞＞書）交该二次函数的图象于另一点C（x】，y】）,交y轴于M.（1）宜接写出A点坐标，并求该二次函数的解析式；（2）过点B作BD丄AC交AC于D,若M（0,3雄）且点Q是线段DC±的一个动点，求出当△DBQIjAAOM相似时点Q的坐标；（3）设P（・l,・2）,图2中连CP交二次函数的图象于另一点E（X2,y2），连AE交y轴于N,请你探究OM・ON的值的变化情况，若变化，求具变化范围；若不变，求其值.\n【分析】(1)由直线y=kx+3k(k>*)过点A,可求出点A的坐标，然后把点A的坐标代(2)根据有两个角相等的三角形相似，可得①ZDQB=ZOMA,®ZDQB=ZA・①根据平行线的判定与性质，可得Q点的横坐标，根据自变量与函数值的对应关系，可得答案；②根据等腰三角形的判定，可得关于m的方程，根据解方程，可得m的值，再根据自变屋与函数值的对应关系，可得答案；(3)直线PC解析式为y=ax+a-2,与抛物线y二gx'+x+l联立得到关于x的一元二次方程,由根与系数的关系知x】+X2=4a-4,xiX2=l1-4a,根据婴段得到OAOAXj_xAx2-xAom«on=4oa2,得到结果为定值2.(2015*武侯区模拟)如图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为(-3,4),点C在x轴的正半轴上，直线AC交y轴于点M,AB边交y轴于点H.(1)求肓线AC的函数关系式；(2)连接BM,动点P从点A出发，沿折线A・B・C方向以2个单位/秒的速度向终点C匀速运动，设APNIB的面积为S(ShO),点P的运动吋间为t秒，求SUtZ间的函数关系式(要求写出自变量t的取值范围).【分析】(1)已知A点的坐标，就可以求II1OA的长，根据OA=OC,就可以得到(2点的坐标，根据待定系数法就可以求出函数解析式.(2)点P的位置应分P在AB和BC±，两种情况进行讨论.当P在AB±时，APNIB的底边PB可以用时间t表示出来，高是MH的长，因而面积就可以表示出来.3.(2015*武侯区模拟)如图(1),ZABC=90°,O为射线BC上一点，OB=4,以点O为圆心，£bO长为半径作OO交BC于点D、E.2(1)当射线BA绕点B顺时针方向旋转36()。，若BA与OO相切时，那么BA旋转了多少度？(2)若射线BA绕点B按顺时针方向旋转与<30相交于M、N两点(如图(2)),MN=2*2,\n【分析】（1）耍求当射线BA绕点B按顺时针方向旋转多少度时与OO相切，就耍先利用切线的性质画岀图形，从图屮可以看出旋转的度数就是ZAZBC的度数.然后利用图形来计算.从图小可看出，OG二OB的一半，所以角PBG二30。，所以当射线BA绕点B按顺时针方向旋转60。或120。吋-UOO相切：（2）由勾股定理边的关系町知弧所对的闘心角是一个直角，然后利用弧长公式计算.2.（2015*武侯区模拟）己知如图，矩形OABC的长OA=V3,宽OC=1,将AAOC沿AC翻折得ZXAPC.（1）求ZPCB的度数；（2）若P,A两点在抛物线y=-|x2+bx+c±,求b,c的值，并说明点C在此抛物线上；（3）（2）中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点，N是y轴上的点，以点E、M、D、N为顶点的四边形是平行四边形，试求【分析】（1）根据OC、OA的长，町求得ZOCA=ZACP=60°（折叠的性质），ZBCA=ZOAC=30°,由此可判断岀ZPCB的度数.（2）过P作PQ丄OA于Q,在RtAPAQ易知PA=OA=3,而ZPAO=2ZPAC=60°,即可求出AQ、PQ的长，进而可得到点P的坐标，将P、A坐标代入抛物线的解析式中，即可得到b、c的值，从而确定抛物线的解析式，然后将C点坐标代入抛物线的解析式中进行验证即可.（3）根据抛物线的解析式易求得C、D、E点的坐标，然后分两种情况考虑：①DE是平行四边形的对角线，由于CD//X轴，且C在y轴上，若过D作直线CE的平行线，那么此直线与x轴的交点即为M点，而N点即为C点，D、E的处标已经求得，结合平行四边形的性质即可得到点M的坐标，而C点坐标已知，即可得到N点的坐标；②DE是平行四边形的边，由于A在x轴上，过A作DE的平行线，与y轴的交点即为N点，而M点即为A点；易求得ZDEA的度数，即可得到ZNAO的度数，已知OA的长，通过解直角三角形可求得ON的值，从而确定N点的坐标，而M点与A点重合，其坐标已知；同理，由于C在y轴上，且CD〃x轴，过C作DE的平行线，也可找到符合条件的M、N点，解法同上.\n2.（2014*成都）如图，在OO的内接AABC屮，ZACB=90°,AC=2BC,过C作AB的垂线1交OO于另一点D,垂足为E.设P是处上异于A,C的一个动点，射线AP交1于点F,连接PC与PD,PD交AB于点G.（1）求证：APACsAPDF；（2）若AB=5,AP=BP,求PD的长；（3）在点P运动过程中，设^=x,tanZAFD=y,求y与x之间的函数关系式.（不要求写BG岀X的取值范围）【分析】（1）证明相似，思路很常规，就是两个角相等或边长成比例.因为题屮因圆周角易知一对相等的角，那么另一对角相等就是我们需要努力的方向，因为涉及圆，倾向于找接近圆的角ZDPF,利用补角在圆内作等量代换，等弧对等角等知识易得ZDPF=ZAPC,则结论易证.（2）求PD的长，且此线段在上问己证相似的△PDF屮，很明显川相似得成比例，再将具他边代入是应有的思路.利用已知条件易得其他边长，则PD可求.（3）因为题II涉及ZAFD与也在第一问所得相似的APDF中，进而考虑转化，ZAFD=ZPCA,连接PB得ZAFD=ZPCA=ZPBG,过G点作AB的垂线，若此线过PB与AC的交点那么结论易求，因为根据三角函数或三角形与三角形ABC相似可用AG表示ZPBG所对的这条高线.但是"此线是否过PB与AC的交点〃？此时百先需要做的是多画儿个动点P,观察我们的猜想.验证得我们的猜想应是正确的，可是证明不能靠画图，如何求证此线过PB与AC的交点是我们解题的关键.常规作法不易得此结论，我们可以换另外的辅助线作法，先做垂线，得交点H,然后连接交点与B,再证明ZHBG=ZPCA=ZAFD.因为C、D关于AB対称，可以延长CG考虑P点的对称点.根据等弧対等角，可得ZHBG=ZPCA,进而得解题思路.3.（2013*荆州）如图，已知:如图①,直线y=-V3x+V3与x轴、y轴分别交于A、B两点，两动点D、E分别从A、B两点同时出发向O点运动（运动到O点停止）；对称轴过点A且顶点为M的抛物线y=a（x・k）2+h（a<0）始终经过点E,过E作EG〃OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位氏度/秒和逅个单位长度/秒，运动时间为t秒.（1）用含t代数式分别表示BF、EF、AF的长;（2）当t为何值时，四边形ADEF是菱形？判断此时厶AFGAAGB是否相似，并说明理由；（3）当AADF是直角三角形，且抛物线的顶点M恰好在BG上时，求抛物线的解析式.\n图①图②【分析】（1）Q先求出一次两数y=-V3x+<3与坐标轴交点A、B的坐标，然后解直角三角形求出BF、EF、AF的长；（2）由EF〃AD,且EF=AD=t,则四边形ADEF为平行四边形，若ADEF是菱形，贝DE=AD=t.由DE=20D,列方程求出t的值;如答图1所示，推H1ZBAG=ZGAF,ZABG=ZAGF=30°,证明Z\AFG・Z\AGB和似.（3）当AADF是直角三角形时，有两种情形，需要分类讨论：①若ZADF=90\如答图2所示•首先求出此时（的值；其次求出点G的坐标，利用待定系数法求出肓线BG的解析式，得到点M的坐标；最示利用顶点式和待定系数法求岀抛物线的解析式；②若ZAFD=90°,如答图3所示.解题思路少①相同.2.（2005*常徳）如图，AB是OO的直径，BC是OO的弦，OO的割线PDE垂直AB于点F,交BC于点G,连接PC,ZBAC=ZBCP,求解下列问题：（1）求证：CP是的切线.（2）当ZABC=30°,BG=2V|,CG=4^时，求以PD、PE的长为两根的一元二次方程.（3）若（1）的条件不变，当点C在劣弧AD±运动时，应再具备什么条件可使结论bg2=bf>bO成立？试写出你的猜想，并说明理由.【分析】（1）连接OC,证ZOCP=90°即可;（2）根据已知条件发现等边三角形CPG,则PC=CG.根据切割线定理求得PD和PE的积;再根据等边三角形的性质和30。的直角三角形的性质求得PD,PE的长，从而写岀方程；（3）要让此结论成立，只要证明厶BFG^ABG0即可，凡是能使△BFGs^BGO的条件都可以.3.（2010*青羊区校级口主招生）已知：抛物线y=x2~（a+b）其中a、b、c是AABC的ZA、ZB、ZC的对边.\n（1）求证：抛物线与x轴必有两个不同交点；（2）设直线y=ax-be与抛物线交于E、F两点，与y轴交于点M,抛物线与y轴交于点N,若抛物线的对称轴为x=a,AMNE与AlVINF的面积比为5：1,求证：AABC是等边三角形；（3）在（2）的条件下，设AABC的面积为施，抛物线与x轴交于点P、Q,问是否存在过P、Q两点且Aiy轴和切的圆？若存在，求出圆的圆心处标，若不存在，请说明理由.【分析】（1）令y=0,用根的判别式和三角形三边关系即可证得；（2）先根据抛物线的对称轴求出a.b的关系.然后联立抛物线与直线1的解析式，求出E、F的横坐标，已知AMNE的而积是△MNF的而积的5倍，根据等底三角形的面积比等于高的比，由此可得出E的横处标是F的横处标的5倍，由此可求出a、c的关系，由此可求出三角形ABC的形状为等边三角形，得证；（3）由（2）得到三角形ABC为等边三角形，根据面积求出等边三角形的边长，即可得到三角形ABC的边长，即得到a=b=c的值，代入确定出抛物线解析式，令解析式屮的y=0,求出x的值，即可得到P和Q的横坐标，确定出两点的坐标，即可求出PQ的长，设圆H为满足题意的鬪，根据P与Q关于对称轴对称，得到HJ垂直于PQ,根据垂径定理得到J为PQ中点,即可求出PJ的长,又圆心H在x=2上，且圆H与y轴相切,得到圆心H的横处标为2,且圆H的半径为2,即HP=2,在直角三角形HPJ中，根据勾股定理求出HJ的长，即为圆心H的纵坐标，写出圆心H坐标即可.2.（2014*武侯区校级自主招生）数独（sudoku）是一种源自18世纪末的瑞士，后在美国发展、并在口木发扬光人的数学智力拼图游戏.拼图是九宫格（即3格宽x3格高）的正方形状，每-•格乂细分为一个九宫格.在每一个小九宫格中，分别填上1至9的数字，让整个大九宫格每一列、每一行的数字都不重复.下面是一个数独游戏，请完成该游戏.（您只需要完整地填出其屮的5个小九宫格即可）（评分标准：完整地填出其中的5个小九宫格Fl.5个均正确即可给满分.未填出5个不给分.若填出超过5个且无错给满分，若填出超过5个且有任何一•处错误不给分.）\n【分析】根据横列、竖列和方格的限制条件排除各个点不可能的数字，并从1-9将各个可能的数字用小字体逐个写进每个空口的格子.然后再进行审查即可.2.（2005・资阳）如图，已知0为坐标原点,ZAOB=30°,ZABO=90°,且点A的坐标为（2,0）.（1）求点B的坐标；（2）若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的解析式；（3）在（2）屮的二次函数图象的OB段（不包括点O、B）上，是否存在一点C,使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明【分析】（1）在RtAOAB中，由ZAOB=30°nJ以得到OBh/f,过点B作BD垂直于x轴,垂足为D,利用已知条件可以求iTiOD,BD,也就求出B的坐标;（2）根据待定系数法把A,B,O三点处标代入函数解析式中就可以求出解析式；（3）设存在点C（x,__?V3x2+±Z3x）y使四边形ABCOffi积最大，而ZXOAB面积为定3_3_值，只要AOBC面积最大，四边形ABCO面积就最大.过点C作x轴的垂线CE,垂足为E,交OB于点F,则Saobc=Saocf+Sabcf=-ICFI•IOEI+-ICFI•IEDI=-ICFI•IODI=-ICFI,ifij\n2224ICFI=yc-yf=-竽-^x=--^x2+<3x,这样可以得到Saobc=-^x2+^x,利用二次函数就可以求出AOBC而积最大值，也可以求出C的朋2_4_标.2.（2005*武汉）已知：如图，直线尸-号x+3交x轴于Oi，交y轴于O2,OO2-Ux轴相切于O点，交直线0102于P点，以Oi为圆心，0]P为半径的圆交x轴于A、B两点，PB交002于点F,OO1的弦BE=BO,EF的延长线交AB于D,连接PA、P0.（1）求证：ZAPO=ZBPO；（2）求证：EF是<302的切线；（3）E0]的延长线交0O]于C点，若G为BC上一动点，以OiG为总径作003交O1C于点M,交OiB于N.下列结论：①0]M・0]N为定值；②线段MN的长度不变.只有一个是正确的，请你判断岀正确的结论，并证明正确的结论，以及求出它的值.【分析】（1）可通过度数來求两角相等.连接O2F,那么ZO2PF=ZO2FP=ZOBP,因此O2F〃AB,这样可得出圆O2的圆心角ZOO2F=9（）°.因此ZOPF=45°,那么ZAPO=90°・45°=45°,因此两角相等.（2）由于（1）小得出了02F〃AB,因此只要证得DE丄AB,就能得出DE丄OqF,也就得出了DE是圆02的切线的结论，那么关键是证明DE丄AB.可通过垂径定理来求.延长ED交G）Oi于点H,那么就要求出DE=DH或BE=BH,那么就要先求出ZBEH二ZBHE.连接PE,那么ZBHE=ZEPB,那么证ZEPB=ZDEB即可•可通过相似三角形BEF和BPE来求得，这两个三角形中，已知了一个公共角，我们再看夹这个角的两组対边是否成比例.山于BO2=BF*BP,而B0二BE,因此BE2=BF*BP,由此可得出两三角形相似，进而可根据前面分析的步骤得岀木题的结论.（3）MN的长度不变.这是因为点G是BC上的一个动点，但的0|C长度是不变的，它等于G）的半径8,另外ZBOiC的大小也是始终不变的，因为所有的003都是等圆，故弧MGN也都是和等的，故弦MN都是相等的，求MN的长，可通过构建全等三角形來求解，过N作003的直径NK,连接MK,那么三角形NKM和EDO]全筹，那么只要求HIDE的长即可，根据直线的解析式，可得出0|,02的坐标，也就求出了00|,002的值，也就能得出圆Oi的半径的长，进而可求Mad,bd的长然后根据de2=ad*db即可得出mn的值.