2014年初中数学中考试卷 9页

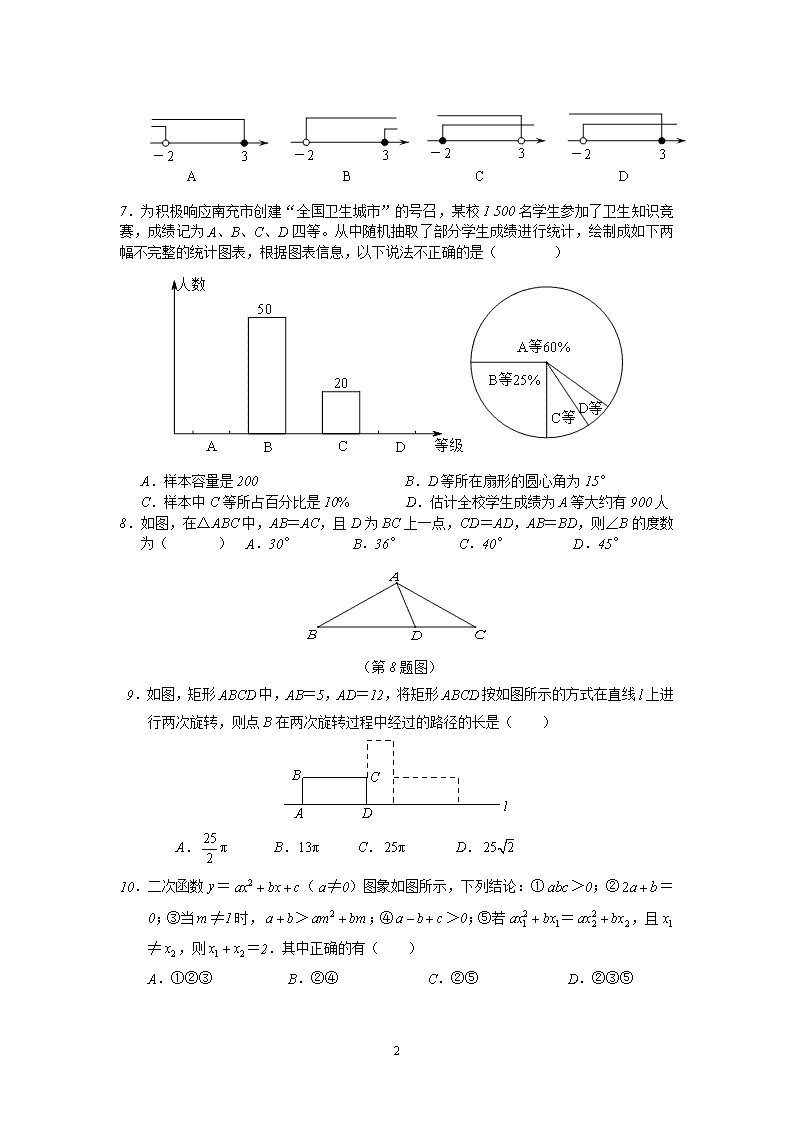
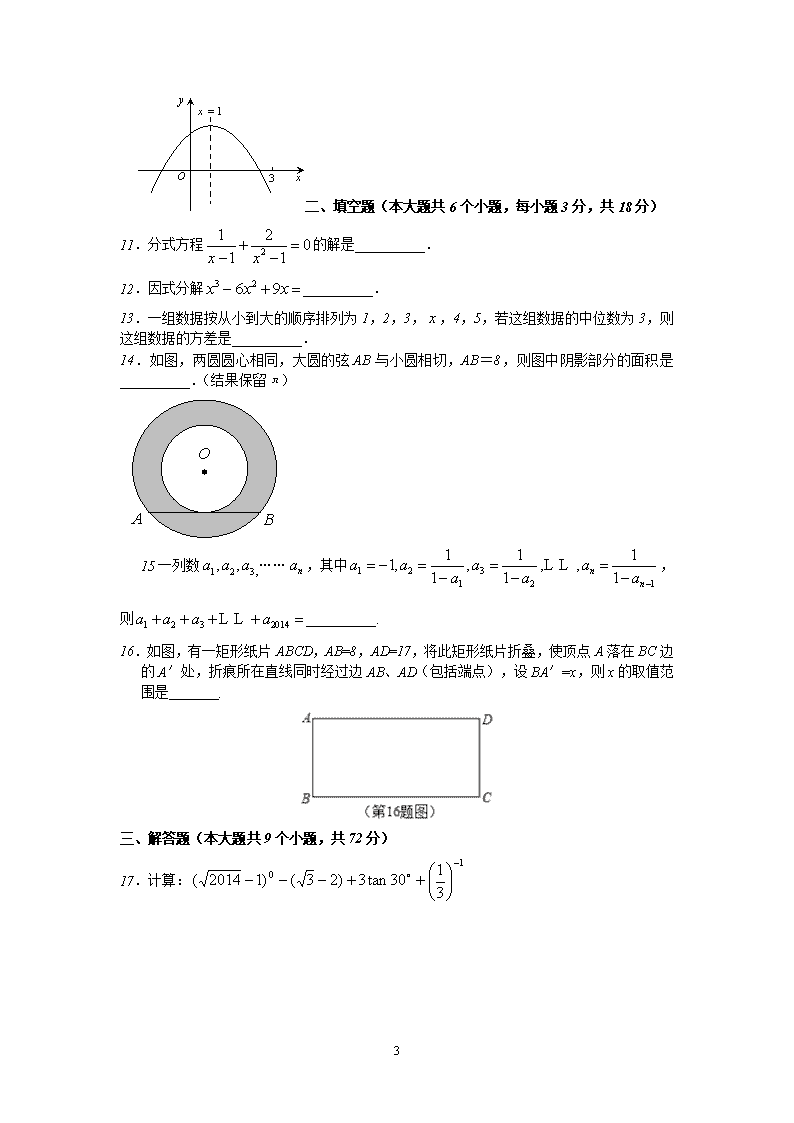
2014年四川省南充市中考数学试卷（满分120分，时间120分钟）一、选择题（本大题共10个小题，每小题3分，共30分）1．的值是（）A．3B．－3C．D．－2．下列运算正确的是（）A．a3.a2=a5B．(a2)3=a5C．a3+a3=a6D．(a+b)2=a2+b23．下列几何体的主视图既是中心对称图形又是轴对称图形的是（）ABCD4．如图，已知∥，，，则的度数为（）（第2题图）A．30°B．32.5°C．35°D．37.5°5．如图，将正方形放在平面直角坐标系中，是原点，的坐标为（1，），则点的坐标为（）A．（－，1）B．（－1，）C．（，１）D．（－，－1）6．不等式组的解集在数轴上表示正确的是（）9\nABCD7．为积极响应南充市创建“全国卫生城市”的号召，某校1500名学生参加了卫生知识竞赛，成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计，绘制成如下两幅不完整的统计图表，根据图表信息，以下说法不正确的是（）A．样本容量是200B．D等所在扇形的圆心角为15°C．样本中C等所占百分比是10%D．估计全校学生成绩为A等大约有900人8．如图，在△ABC中，AB＝AC，且D为BC上一点，CD＝AD，AB＝BD，则∠B的度数为（）A．30°B．36°C．40°D．45°（第8题图）9．如图，矩形ABCD中，AB＝5，AD＝12，将矩形ABCD按如图所示的方式在直线上进行两次旋转，则点B在两次旋转过程中经过的路径的长是（　　）A．B．C．D．10．二次函数＝（≠0）图象如图所示，下列结论：①＞0；②＝0；③当≠1时，＞；④＞0；⑤若＝，且≠，则＝2．其中正确的有（　　）A．①②③B．②④C．②⑤D．②③⑤9\n二、填空题（本大题共6个小题，每小题3分，共18分）11．分式方程的解是__________．12．因式分解__________．13．一组数据按从小到大的顺序排列为1，2，3，，4，5，若这组数据的中位数为3，则这组数据的方差是__________．14．如图，两圆圆心相同，大圆的弦AB与小圆相切，AB＝8，则图中阴影部分的面积是__________．（结果保留π）OBA15一列数……，其中，则__________.16．如图，有一矩形纸片ABCD，AB=8，AD=17，将此矩形纸片折叠，使顶点A落在BC边的A′处，折痕所在直线同时经过边AB、AD（包括端点），设BA′=x，则x的取值范围是.三、解答题（本大题共9个小题，共72分）17．计算：9\n18.如图，AD、BC相交于O，OA=OC，∠OBD=∠ODB.ABOCD（18题图）求证：AB=CD.19．（8分）在学习“二元一次方程组的解”时，数学张老师设计了一个数学活动.有A、B两组卡片，每组各3张，A组卡片上分别写有0，2，3；B组卡片上分别写有－5，－1，1.每张卡片除正面写有不同数字外，其余均相同.甲从A组中随机抽取一张记为x，乙从B组中随机抽取一张记为y.（1）若甲抽出的数字是2，乙抽出的数是－1，它们恰好是ax－y=5的解，求a的值；（2）求甲、乙随机抽取一次的数恰好是方程ax－y=5的解的概率.（请用树形图或列表法求解）20.(8分)已知关于x的一元二次方程x2－2x+m=0,有两个不相等的实数根.⑴求实数m的最大整数值；⑵在⑴的条下，方程的实数根是x1，x2,求代数式x12+x22－x1x2的值.21．(8分)如图，一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A(2,5)和点B,与y轴相交于点C(0，7).(1)求这两个函数的解析式；(2)当x取何值时，＜.OxBACy752（第21题图）9\n22.(8分)马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息，可疑漂浮物P在救助船A的北偏东53.50方向上，在救助船B的西北方向上，船B在船A正东方向140海里处。（参考数据：sin36.5≈0.6,cos36.5≈0.8,tan36.5≈0.75）.(1)求可疑漂浮物P到A、B两船所在直线的距离；（2）若救助船A、救助船B分别以40海里/时，30海里/时的速度同时出发，匀速直线前往搜救，试通过计算判断哪艘船先到达P处。ABP东北（第22题图）23、（8分）今年我市水果大丰收，A、B两个水果基地分别收获水果380件、320件，现需把这些水果全部运往甲、乙两销售点，从A基地运往甲、乙两销售点的费用分别为每件40元和20元，从B基础运往甲、乙两销售点的费用分别为每件15元和30元，现甲销售点需要水果400件，乙销售点需要水果300件。（1）设从A基础运往甲销售点水果x件，总运费为w元，请用含x的代数式表示w,并写出x的取值范围；（2）若总运费不超过18300元，且A地运往甲销售点的水果不低于200件，试确定运费最低的运输方案，并求出最低运费。24.如图，已知AB是⊙O的直径，BP是⊙O的弦，弦CD⊥AB于点F，交BP于点G，E在CD的延长线上，EP=EG,(1)求证：直线EP为⊙O的切线；9\n(2)点P在劣弧AC上运动，其他条件不变，若BG²=BF·BO.试证明BG=PG.(3)在满足(2)的条件下，已知⊙O的半径为3，sinB=.求弦CD的长.（第24题图）25.如图，抛物线y=x²+bx+c与直线y=x－1交于A、B两点.点A的横坐标为－3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D.(1)求抛物线的解析式；（2）当m为何值时，；(3)是否存在点P,使△PAD是直角三角形，若存在，求出点P的坐标；若不存在，说明理由.APDBCOy（第25题图）x9\n2014年南充市数学中考试卷答案一，选择题：1、C2、A3、D4、C5、A6、D7、B8、B9、B10、D二、填空题：11、x=-312、13、14、16π15、16、三、解答题：17、解：=1-+3+=1-++3=618、证明：∵∠OBD=∠ODB.∴OB=OD在△AOB与△COD中，∴△AOB≌△COD（SAS）∴AB=CD.20、解：⑴由题意，得：△＞0，即：＞0，m＜2，∴m的最大整数值为m=1（2）把m=1代入关于x的一元二次方程x2－2x+m=0得x2－2x+1=0，根据根与系数的关系：x1+x2=2，x1x2=1，∴x12+x22－x1x2=（x1+x2）2－3x1x2=（2）2－3×1=521、解：∵反比例函数y2=的图象过点A(2,5)∴5=，m=10即反比例函数的解析式为y=。∵一次函数y1=kx+b的图象过A(2,5)和C(0，7).∴5=2k+7，k=-1即一次函数解析式为y=-x+7(2)解方程组得或∴另一交点B的坐标为(5，2).根据图象可知，当x＜2或x＞5时，＜.9\n22、解：（1）如图，过点P作PH⊥AB于点H，则PH的长是P到A、B两船所在直线的距离.根据题意，得∠PAH=90°－53.50°=36.5°，∠PBH=45°，AB=140海里.设PH=x海里在Rt△PHB中，tan45°=，∴BH=x；在Rt△PHA中，tan36.5°=，∴AH==x.∵AB=140，∴x+x=140，解得x=60，即PH=60，因此可疑漂浮物P到A、B两船所在直线的距离为60海里.（2）在Rt△PHA中，AH=×60=80，PA==100，救助船A到达P处的时间tA=100÷40=2.5小时；在Rt△PHB中，PB==60，救助船B到达P处的时间tB=60÷30=2小时.∵2.5<2，∴救助船A先到达P处.23、解：（1）依题意，列表得A（380）B（320）甲（400）x400-x乙（300）380-x320-(400-x)=x-80∴W=40x+20×(380-x)+15×(400-x)+30×(x-80)=35x+11200又解得80≤x≤380(2)依题意得解得，∴x=200,201,202因w=35x+10,k=35，w随x的增大而增大，所以x=200时，运费w最低，最低运费为81200元。此时运输方案如下：AB甲200200乙18012025、解：1）由已知得，，，∴，解得，∴.9\n（2）∵，，∴.∵，即，∴.当点P运动至A处，此时P、D重合.①当PD在点A左侧时，，则，解得，.②当PD在点A右侧时，，则，解得，，不合题意，舍去.综上，，或.（3）∵，∴当或时，△PAD是直角三角形.①若，则AP∥x轴，∴，即，解得，，∴；②若，AP⊥AB.又直线AP：，由，解得，，∴.综上，或.9