“数与式”复习策略_中考_初中教育_教育专区 11页

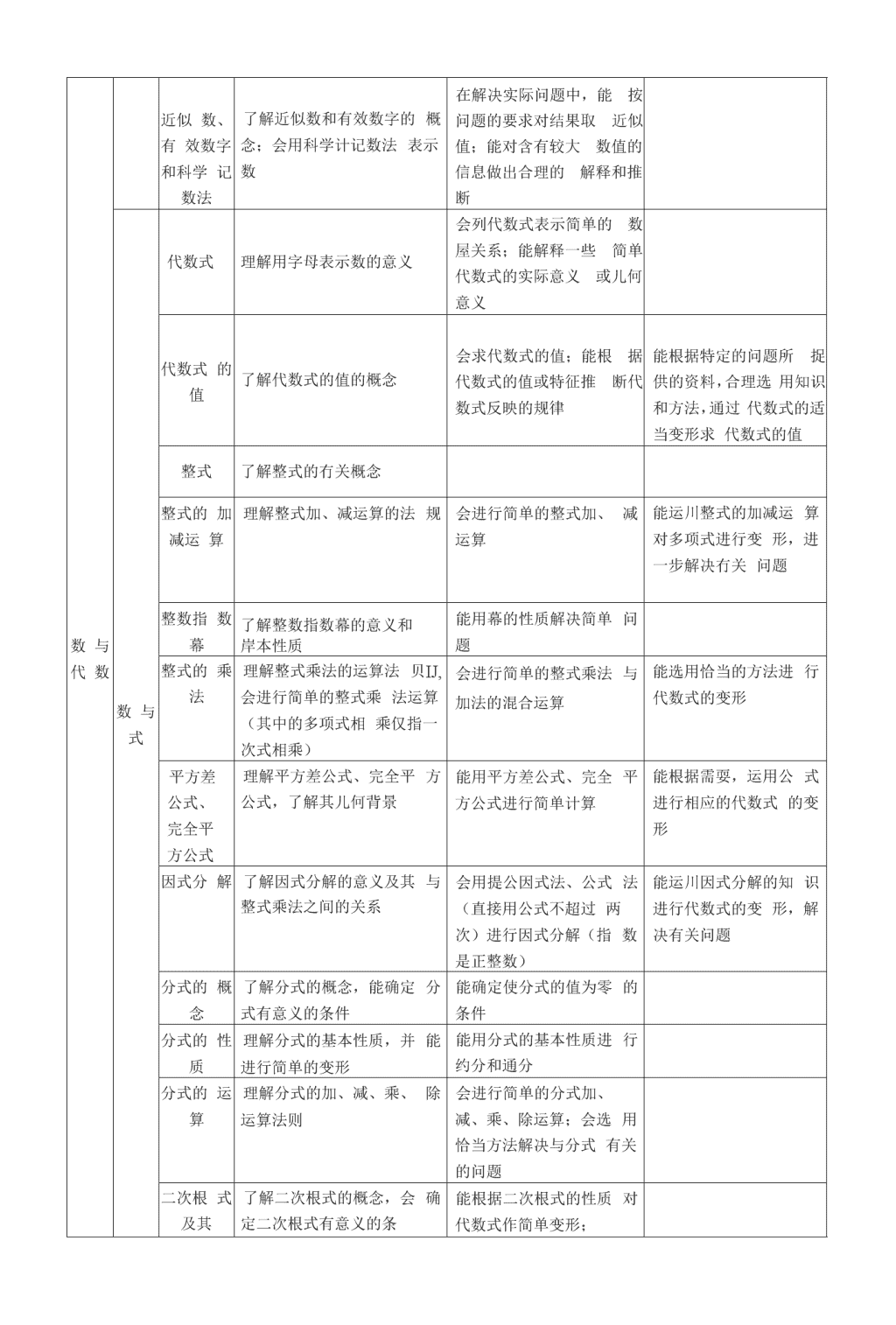
“数与式”复习西城实验学校李亚平2012.2.23数与式的内容包括实数、整式、分式和二次根式，这部分内容的特点是概念多、性质多、运算法则多、技能性强.这部分知识的很大一部分是数运算、式运算与式的变形等方面的技能，体现转化思想和类比思维。它是初中数学的基础，是所有解方程（组）、不等式（组），解决概率和统计等冇关计算问题的棊础，而还是许多图形问题中冇关数量表达的棊础•因此耍重视这部分的复习，做到会做的题不丢分.数与式这部分内容在2006、2007>2008、2009、2010>2011/\年的北京市中考题中直接考查这部分知识的题冃分别占了34分、39分、34分、26分、29分、34分，因此，复习时耍充分重视.一、中考考试要求考试内容考试要求层次ABC数与代数数与式有理数理解有理数的意义会比鮫有理数的大小无理数了解无理数的概念能根据要求用有理数估计一个无理数的大致范围平Jj根、算术平方根了解开方与乘方互为逆运算，了解平方根及算术平方根概念，会用根号表示非负数的平方根及算术平方根会用平方运算的方法，求某些非负数的平方根立方根了解立方根的概念，会用根号表示数的立方根会用立方运算的方法，求某些数的立方根实数了解实数的概念会进行简单的实数运算数轴能用数轴上的点表示有理数；知道实数与数轴上的点一一对应相反数会用有理数表示具有和反意义的量，借助数轴理解相反数的意义，会求实数的相反数掌握相反数的性质绝对值借助数轴理解绝对值的意义，会求实数的绝对值会利用绝对值的知识解决简单的化简问题和计算问题有理数的运算理解乘方的意义掌握有理数的加、减、乘、除、乘方及简单的混合运算（以三步为主）能运用有理数的运算解决简单问题运算律理解有理数的运算律能用运算律简化有理数运算\n数与代数近似数、有效数字和科学记数法了解近似数和有效数字的概念；会用科学计记数法表示数在解决实际问题中，能按问题的要求对结果取近似值；能对含有较大数值的信息做出合理的解释和推断数与式代数式理解用字母表示数的意义会列代数式表示简单的数屋关系；能解释一些简单代数式的实际意义或儿何意义代数式的值了解代数式的值的概念会求代数式的值；能根据代数式的值或特征推断代数式反映的规律能根据特定的问题所捉供的资料，合理选用知识和方法，通过代数式的适当变形求代数式的值整式了解整式的冇关概念整式的加减运算理解整式加、减运算的法规会进行简单的整式加、减运算能运川整式的加减运算对多项式进行变形，进一步解决冇关问题整数指数幕了解整数指数幕的意义和岸本性质能用幕的性质解决简单问题整式的乘法理解整式乘法的运算法贝IJ,会进行简单的整式乘法运算（其中的多项式相乘仅指一次式相乘）会进行简单的整式乘法与加法的混合运算能选用恰当的方法进行代数式的变形平方差公式、完全平方公式理解平方差公式、完全平方公式，了解其儿何背景能用平方差公式、完全平方公式进行简单计算能根据需耍，运用公式进行相应的代数式的变形因式分解了解因式分解的意义及其与整式乘法之间的关系会用提公因式法、公式法（直接用公式不超过两次）进行因式分解（指数是正整数）能运川因式分解的知识进行代数式的变形，解决有关问题分式的概念了解分式的概念，能确定分式有意义的条件能确定使分式的值为零的条件分式的性质理解分式的基本性质，并能进行简单的变形能用分式的基本性质进行约分和通分分式的运算理解分式的加、减、乘、除运算法则会进行简单的分式加、减、乘、除运算；会选用恰当方法解决与分式有关的问题二次根式及其了解二次根式的概念，会确定二次根式有意义的条能根据二次根式的性质对代数式作简单变形；\n性质件能在给定条件下，确定字母的值二次根式的化简和运算理解二次根式的加、减、乘、除运算法则会进行二次根式的化简，会进行二次根式的混合运算（不要求分母有理化）二、2009—2011年中考命题规律总结（-）实数内容知识点分项细冃()9年10年11年考试要求ABC实数基木概念1.实数的分类V数轴2.数轴上的点与实数的对应关系V平方根、算术平方根及立方根3.平方根、算术平方根的概念V4.利用根号表示非负数的平方根、算术平方根及立方根V相反数、绝对值及倒数5.相反数的意义及求法选择1题V6.实数绝对值的求法选择1题V7.倒数的意义及求法选择1题科学记数法、有效数字、近似数8.近似数、有效数字的概念，利用科学记数法表不数选择2题选择2题选择2题V数的大小比较9.实数的大小比较，估计无理数的人小V实数的运算10.运算法则和运算律解答13题解答13题解答13题V11•能运用有理数的运算解决简单问题V科学记数法与实数的运算是必考内容，且科学记数法一般都在选择题屮出现，实数的运算在解答题第13题出现；选择题第1题一燉考查相反数、绝对值及倒数的定义，这三个知识点在历年中考题中交替出现；平方根、算术平方根的内容一般与勾股定理等知识相结合考查；运用有理数的运算解决简单问题近儿年在综合题中有所体现.近三年都考查了科学记数法，主耍以社会热点问题作为命题的背景；近三年考卷中的第13题主要以绝对值、零指数鬲、负指数幕、二次根式的化简、特殊角的三角函数值等运算\n为重要考点.（二）整式的运算、乘法公式内容知识点分项细目09年10年11年考试要求ABC整式的%—算、乘法公式整式运算1.幕的运算2.整式的加减、乘除混合运算V乘法公式3.平方差公式V4.完全平方公式填空11题V因式分解5.利用提公因式法和公式法分解因式选择7题填空10题填空10题V因式分解是每年川考必考内容，一般出现在选样题、填空题当川.乘法公式也是常考内容，对于整式的运算，i般体现在综合题的解题过程中，所以在复习中耍引起足够重视.近三年考题中对因式分解的考查中，设计的题冃都是先提取公因式，再利用公式法解题.近三年考题中基础题部分有关乘法公式的考查，一是因式分解中逆用乘法公式，二是利用乘法公式将代数式变形.（三）分式、二次根式的概念与运算内容知识点分项细目09年10年11年考试要求ABC整式的运算、乘法公式分式的概念及性质1.能确定分式有意义或值为零的条件填空9题V2.利用分式的基本性质进行约分和通分J分式的运算3.分式的加、减、乘、除运算V次根式二次根式及其性质4.二次根式有意义的条件，确定字母的值填空9题V二次根式的运算5.1次根式的加、减、乘、除混合运算V对分式、二次根式的考杳内容主要是确定分式有意义或值为零的条件，确定二次根式有意义的条件.二次根式的性质及化简主要结合实数运算进行.（四）求代数式的值\n内容知识点分项细冃09年10<111年考试要求ABC求代数式的值求代数式的值1.会求代数式的值2.通过代数式的适当变形求值解答16题解答15题V求代数式的值是常考内容，题空以解答题为主，一•般出现在解答题笫15题或16题的位置上，而在综合题的解答过程中，冇时也冇通过适当变形求代数式值的问题，应予以重视.近三年屮考题以有关条件求值作为常考题型.一类问题是以非负数为载体命题；一类问题是以方程为条件，结合代数式的恒等变形整体带入求值.北京市中考主要考点：1.相反数，倒数，绝对值等有理数有关的概率；2.科学计数法；3.分式与二次根式有意义的条件与分式值为零的条件；4.简单的因式分解；5.含有整数指数幕（0次或负1次）、无理数化简、特殊三角函数值在内的综合运算；6.绝对值与平方数及二次根式的非负性；7.条件求值；（整式与分式的运算）8.新型题：找规律及用代数式表示规律的问题；9.二次多项式的配方变形。三、“数与式”的考法分析“数与式”主要包括数与式的冇关概念和运算，用数或式表示各种情境中的数量及数虽关系，它们是初中数学小最为基础的内容，在中考试卷中也大都以容易题和中档题的形式出现.最近儿年出现了“以数与式的知识为载体考查数学思考和数学学习能力”的新题型.（一）考查“数与式”的基础知识和基本技能1.考查对数与式基本概念的理解例1题1（2010北京）：-2的倒数是（)AA.-1B.丄C.-2D.222题2：写出一个比-1人的负有理数是，比-1人的负无理数是•题3（2007北京）：若1加+2丨+（〃一1）2=0,则m+2n的值为（）CA.-4B・-1C.OD.4题4（2011北京）:我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665575306人。将665575306用科学记数法表示（保留三个有效数字）约为（）CA.66.6xl07B.0.666xl08C.6.66xlO8D.6.66xlO7评析：题1考查是否真正理解了倒数的概念；题2以开放的方式来考查有理数和无理数的概念及大小关系；题3考查了“绝対值”和“平方数”的非负性质，以及绝对值的意义和“相反数”的意义；题4考查了科学记数法与有效数字的概念.凸显所考知识的“基础性”及具基本的认知要求，是这4道题的共同特点.2.考查对数与式有关性质的掌握\n例2题1：如图，在数轴上表示实数的点可能是（）CA.占p八、、鼻B•点QC•点MD•点NPQN0123M4题2（2E海淀—肌若分式占冇意义，则兀的取值范围是—.24题3：已知J2:VI-aa,则d的取值范围是（)cA.a<0B.a<0C.O<€Z<1D.a>0评析:题1考杏实数的人小关系以及在数轴上的表示;题2考杳分式在什么悄况下有意义;题3考查平方根的意义和性质.3道题都是围绕着基木性质，构题简明，II标明确.2.考查对数与式运算法则的掌握例3题1（2011平谷一模）：下列运算正确的是（）AA.2兀兀~=6兀4B.2,x~—3x~=—1C.2,x^-i-3x~=—x~D.2兀〜+3x~=5兀"3题2：化简a+b+（a—b）的最后结果是（）CA.2a+2bB.2bC.2aD.0题3：下列计算错误的是（）DA.—（—2）=2B.V8=2^2C.2x2+3x2=5x2D.（a2）3=a5评析：数、式的运算法则是极为重要的基础知识，有必要进行针对性的考查.本例3道题以不同的方式考査了掌握运算法则和运算性质的情况.3.考查数与式的运算及变形的技能例4题1：若兀=需一JF,y=4a+y/b,则厂的值为（）DA.2y/~aB.C.a+hD.a-b题2：给出3个多项式：X=2a2+3ah+b2,Y=3a2+3abfZ=/+ab,请你任选两个进行加（或减）法运算，再将结果分解因式.题3（2011西城一模）：分解因式：x2y-6xy+9y=题4帥东城-模）：先化简，再求值：（啓+^2；^其中"炉1・（■,1"x+1题5（2011丰台二模）：己知x2+3x=15,求代数式-2x（x-1）+（Zy+1）2的值.\n(2x-+6x+1,31)评析：掌握数与式的运算及变形技能，是学习数与式的重要目的之一，也是提高运算能力的重要基础.题1考查乘法公式的拓广应川；题2考查学牛在给定条件下白主构题，进行加（或减）法运算示再进行因式分解；题3考杏用提公因式与公式法分解因式；题4考杏将分式运算化简后再代入求值；题5考查将整式化简后整体代入求值.这样的题hl既冇对运算规范的耍求，也有对运算灵活运用的耍求.例5题1：如果x+y=-4,x-y=8,那么代数式x2-y2的值是-32题2（2011平谷一模）：已知丄-丄=3,则代数式2兀_14与_2）：的值为以xyx-2xy_y题3（西城二模）：已知x2+xy=i2,xy+y2=15,求代数式（兀+-2y（x+y）的值.-3评析：这样的题以较为综合的形式，考杏灵活运用式的运算法则进行适当变形，不仅考杳了运算能力，也在一定程度上考査了运用知识分析和解决问题的能力.2.考查基本的列式能力例6（1）对单项式“5兀”，我们可以这样解释：香蕉每千克5元，某人买了兀「克，共付款5兀元.请你对“5x”再给出另一个实际生活方面的合理解释：.（2）观察表格一，寻找规律.表格二和表格三分别是从表格一中选取的一部分，则。+方的值为•370123•••1357•••25811•••371115••••••••••••••••••表格一1114a表格二|11|13|表格三评析：列出代数式表达各种情境中的数量及数量关系，是学习“数与式”极为重要的忖的.以上两题所考查的就是这个冃的所对应的列式能力.题1的特点是开放性，体现了代数式的抽象性（在某种程度上也是数学抽象性的农现）；题2的特点是考查发现表格-的行、列的呈现规律，再有表格二和表格三确定出d、〃的值.这样的题针对性强，突出了列代数式的重要性.（二）以“数与式”的知识和性质为载体，考查数学思考和数学学习能力1.将图形与式结合，考查数形结合的思考能力例7题1：如图所示，在长和宽分别是0、b的矩形纸片的四个角都剪去一个边长为X的正方形.（1）用Q、b、X表示纸片剩余部分的面积；(2)当a-6,h-4f且剪去部分的而积等于剩余部分的面积时，求正方形的边长.\n解：（1）ab—4x2；（2）依题意冇：ab—4x2=4x2将a=6,b=4»代入上式，得x2=3,解得兀［=a/3,x2=-石（舍去）.即正方形的边长为巧.题2：如图，C为线段BD±一动点，分别过点B、D作AB丄BD,ED1BD,连结AC、EC.已知AB=5,DE=1,BD=8,设CD二兀.（1）用含x的代数式表示AC+CE的长.（2）请问点C满足什么条件时，AC+CE的值最小？（3）根据（2）中的规律利结论，请构图求出代数式J?+4+J（12—兀）2+9的最小值.解:（1）J（8-兀）-+25+J兀2+1；（2）当昇、aE三点共线时AC+CE的值最小；⑶如下图所示，作BD=12,过点B作ABIBD,过点〃作EDIBD,使AB=2,妙3,连结AE交妙于点C.AE的长即为代数式Jx"+4+J(12-x)~+9的最小值.过点A作AF//血交肋的延氏线于点卜；得矩形ABDF,则AB=DR2,A庄BD=8.所以AE二J12?+（3+2）2=13即J/+4+7（12-x）2+9的最小值为13.题3（2011昌平一模）：现场学习题问题背景：在AABC中，AB、BC、AC三边的长分别为血、辰、币，求这个三角形的而积.小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1）,再在网格中画出格点△4BC（即△43C三个顶点都在小正方形的顶点处），如图1所示.这样不需求AABC的高，而借用网格就能计算出它的面积.\nIL一一4_—LILIUIL—|IB|||IIIIIIUILIUILIL______I」—」」1」1」______—LILI」—」—」—」L（1）请你将AABC的面积直接填写在横线上.思维拓展：（2）我们把上述求△A3C面积的方法叫做构图法.若A/IBC三边的长分别为血d、2屆、426a（a>Q），请利用图2的正方形网格（每个小正方形的边长为a）画出相应的△ABC,并求出它的面积是:探索创新：⑶若△ABC三边的长分别为a/W+a?、V16m2+n2、2yjm2+n2（m>0,n>o,tn^n）,请运用构图法在图3指定区域内画出示意图,并求出AABC的而积为:答案：11LL1L1L1L11L151111111(1)(2)LLLLLL1—111111厂12L_L_L_L_L士面积：3«2.L_・L_L_L_IIIIRIIIIL_L_L_L_L_L_I图2图3而积：3mn.评析：这两道题以式的建立和表达为基础，把图形直观和其屮蕴含的数屋关系与式的表达有机地结合起来，考杳运用代数与几何的相关知识解决问题.题1的（1）肓接要求列式，（2）可有直接列式求得，也可借助列出方程求得，主耍考查的都是列式的能力；题2的（1）直接耍求列式，（2）耍借助“两点的所有连线中线段最短”来求得相应的最小值,（3）则是依据给出的代数式构造出类似于满足（2）的那样的儿何图形借以求出原式的最小值，突现了数形结合的重要意义和作用；题3主要考查利用网格构图求而积方法.这三道题既突出了对数形结合思想的考杳，又突出了对分析问题与解决问题能力的考查.\n2.对数与式进行深入探究，考查知识的关联和思维的深刻性例8题1：若实数a、b满足Q+/异=1,贝屹/+7戸的最小值是.2题2：已知加Fl.m>〃均为止整数,那么下列3个叙述：①在D的“分解”中最大的数是11；②在4?的“分解”中最小的数是13；③若加彳的“分解”屮最小的数是23,④则加等于5.其中正确的是②—如果将加〃进行如下方式的“分解”,3579<<342233252729□□□43评析：题1主要考杳式的表达及变形，以及一个字母的代数式的函数意义；题2主要考查数的一-种特殊的分解.两题对知识的关联和转化的考杳，以及对观察能力和分析问题能力的考查，都有较高的耍求.这样的题口有助于日常教学重视学生思维的广阔性和深刻性.3・借助发现规律，考查归纳思考的能力例9题1：用同样人小的黑色棋了按图（1）、（2）、（3）所示的方式摆图形，按照这样的规律摆下去，则第斤个图形需棋了枚.（用含〃的代数式表示）3,7+1(1)(2)(3)题2：如图，第（1）个多边形由正三角形〃扩展〃而來，边数记为a3,.第（2）个多边形由正方形〃扩展〃而来，边数记为①，…，依此类推，由正n边形〃扩展〃而来的多边形的边数记为第一步：取一个自然数®=5,计算1得％;第二步：算出⑷的各位数字Z和得弘，计算山+i得心:\n第三步:算出色的各位数字之和得®，计算如2+1得如；依次类推，贝IJ。2008二.26题3（2011密云二模）：设四边形ABCD是边长为1的正方形，以正方形ABCD的对和线AC为边作第二个正方形ACEF,再以第二个正方形的对角线厶AE为边作第三个正方形AEGH,如此下去…….E正方形的边长依次为…，an9求（1）记正方形ABCD的边长为q=l,按上述方法所作的（2）根据以上规律写出笫〃个正方形的边长色的表达式・（n21）（a?是口然数）答案:（1）=1=（72）°,^=（5/2/,a3=2=（V2）2,印=2（血）=（血）3,(2)an21)评析：这类试题需借助操作与归纳思考，用代数式表示出情境所蕴含的规律.正确解答这样的题的基础在于对•所给的示例进行观察、操作、対比与分析，从中归纳与概括出所体现的规律来•因此，这类题是考查合情推理的常用手法.四、复习建议1.依据课标及考试说明的要求对知识进行全面复习，控制难度；2.强调解题格式，分专题进行复习；3.要引起学生的足够重视，要求到位，强调落实；4.要注意数学思想和方法的渗透.（数学方法：待定系数法、配方法、换元法.数学思想：数形结合、分类讨论、方程与函数、转化等）。五、“数与式”复习课时计划