初中数学教学论文 中考压轴题解题方法（三） 10页

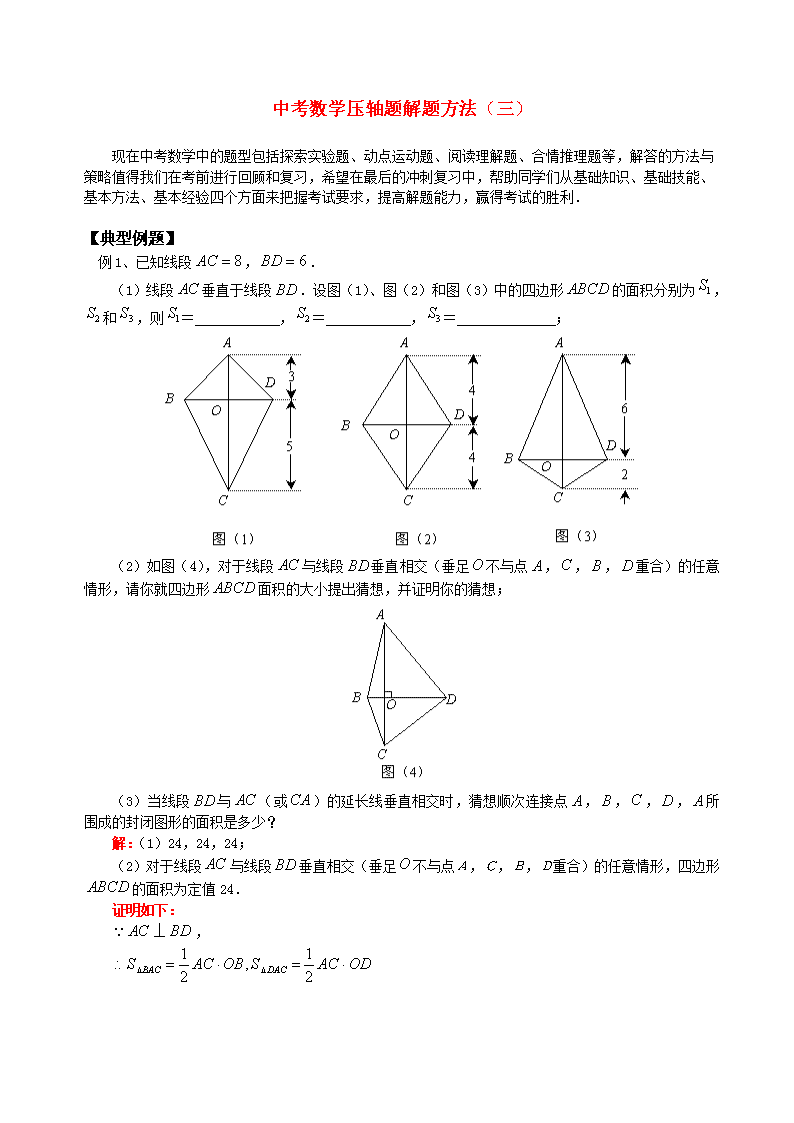
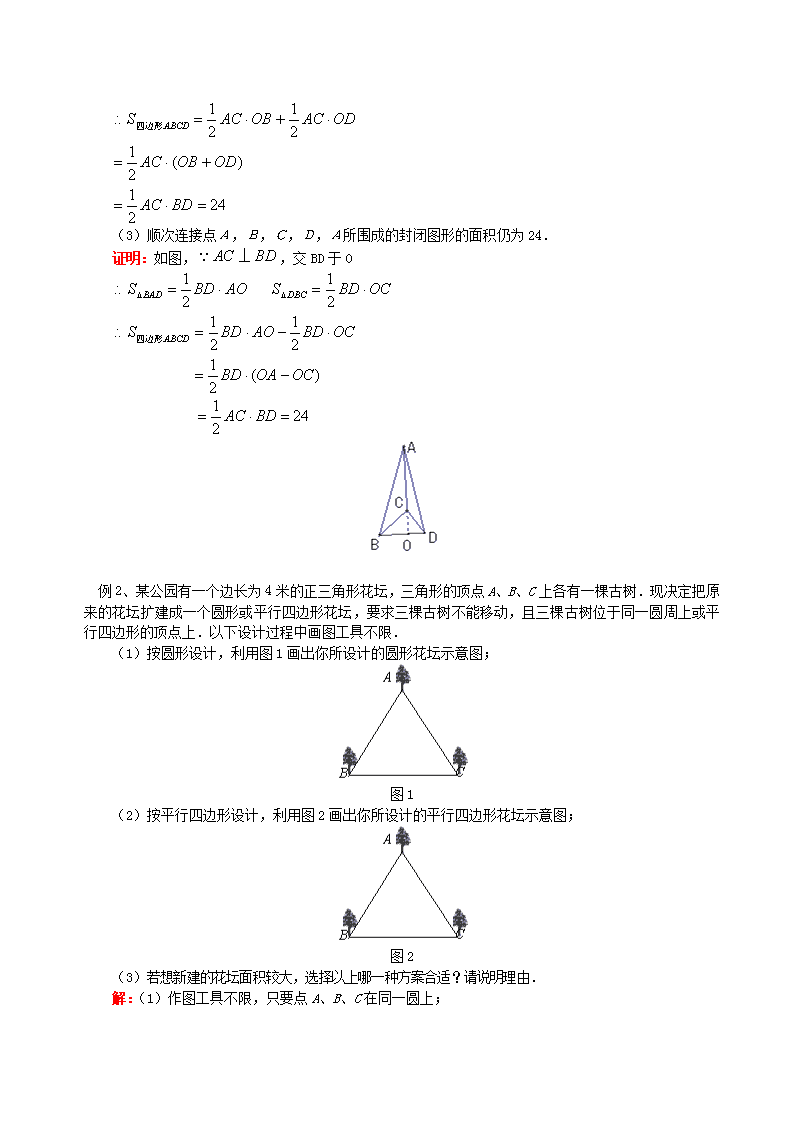
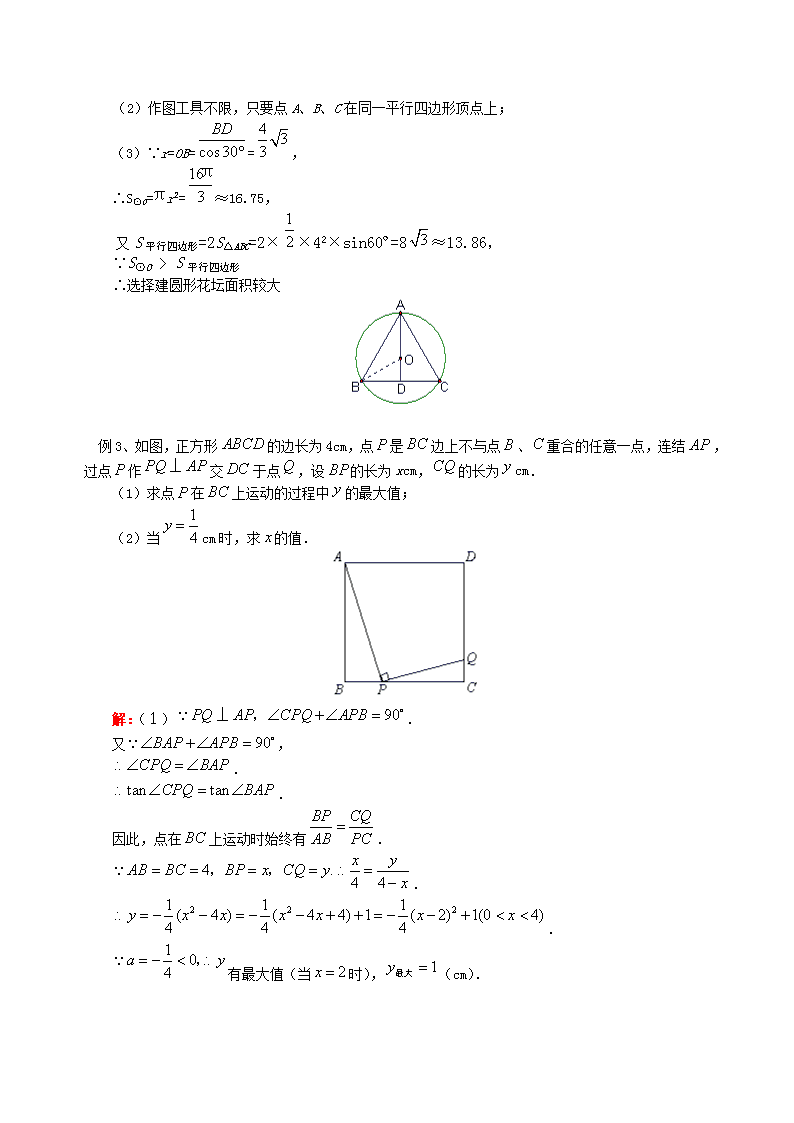
中考数学压轴题解题方法（三）　现在中考数学中的题型包括探索实验题、动点运动题、阅读理解题、合情推理题等，解答的方法与策略值得我们在考前进行回顾和复习，希望在最后的冲刺复习中，帮助同学们从基础知识、基础技能、基本方法、基本经验四个方面来把握考试要求，提高解题能力，赢得考试的胜利．【典型例题】例1、已知线段，．（1）线段垂直于线段．设图（1）、图（2）和图（3）中的四边形的面积分别为，和，则＝　　　　　　，＝　　　　　　，＝　　　　　　　；（2）如图（4），对于线段与线段垂直相交（垂足不与点，，，重合）的任意情形，请你就四边形面积的大小提出猜想，并证明你的猜想；（3）当线段与（或）的延长线垂直相交时，猜想顺次连接点，，，，所围成的封闭图形的面积是多少？解：（1）24，24，24；（2）对于线段与线段垂直相交（垂足不与点Ａ，Ｃ，Ｂ，Ｄ重合）的任意情形，四边形的面积为定值24．证明如下：，\n（3）顺次连接点Ａ，Ｂ，Ｃ，Ｄ，Ａ所围成的封闭图形的面积仍为24．证明：如图，，交BD于O例2、某公园有一个边长为4米的正三角形花坛，三角形的顶点A、B、C上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于同一圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．（1）按圆形设计，利用图1画出你所设计的圆形花坛示意图；图1（2）按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；图2（3）若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由．解：（1）作图工具不限，只要点A、B、C在同一圆上；\n（2）作图工具不限，只要点A、B、C在同一平行四边形顶点上；（3）∵r=OB==，∴S⊙O=r2=≈16.75，又S平行四边形=2S△ABC=2××42×sin60º=8≈13.86，∵S⊙O>S平行四边形∴选择建圆形花坛面积较大例3、如图，正方形的边长为4cm，点是边上不与点、重合的任意一点，连结，过点作交于点，设的长为xcm，的长为cm．（1）求点在上运动的过程中的最大值；（2）当cm时，求的值．解：（１）．又，．．因此，点在上运动时始终有．．．有最大值（当时），（cm）．\n（2）由（１）知，，当cm时，，整理，得　，．，当cm时，的值是cm或cm．【模拟试题】（答题时间：30分钟）1、如图（1），（2），四边形是正方形，是延长线上一点．直角三角尺的一条直角边经过点，且直角顶点在边上滑动（点不与点，重合），另一条直角边与的平分线相交于点．（1）如图（1），当点在边的中点位置时：①通过测量，的长度，猜想与满足的数量关系是　　　　　；②连接点与边的中点，猜想与满足的数量关系是　　　　　；③请证明你的上述两个猜想．（2）如图（2），当点在边上的任意位置时，请你在边上找到一点，使得，进而猜想此时与有怎样的数量关系．2、操作示例对于边长均为的两个正方形，按图（1）所示的方式摆放，再沿虚线，剪开后，可以按图中所示的移动方式拼接为图（1）中的四边形．从拼接的过程容易得到结论：\n①四边形是正方形；②．实践与探究（1）对于边长分别为的两个正方形，按图（2）所示的方式摆放，连结，过点作，交于点，过点作，过点作，．①证明四边形是正方形，并用含的代数式表示正方形的面积；②在图（2）中，将正方形沿虚线剪开后，能够拼接为正方形．请简略说明你的拼接方法（类比图（1），用数字表示对应的图形）．（2）对于个任意的正方形，能否通过若干次拼接，将其拼接为一个正方形？请简要说明你的理由．3、如图1，中，，cm，矩形的长和宽分别为8cm和2cm，点和点重合，和在一条直线上．令不动，矩形沿所在直线向右以每秒1cm的速度移动（如图２），直到点与点重合为止．设移动秒后，矩形与重叠部分的面积为．求与之间的函数关系式．4、如图，形如量角器的半圆O的直径DE=12cm，形如三角板的△ABC中，∠ACB=90°，∠ABC=30°，\nBC=12cm．半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t（s），当t=0s时，半圆O在△ABC的左侧，OC=8cm．（1）当t为何值时，△ABC的一边所在的直线与半圆O所在的圆相切？（2）当△ABC的一边所在的直线与半圆O所在的圆相切时，如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积．\n【试题答案】1、解：（1）①；②．③证明：四边形是正方形，点，分别为，的中点，　　（2）在边上截取（或截取），连接，点就使得成立（图略）．此时，．2、（1）①证明：由作图的过程可知四边形是矩形．在Ｒt△与Ｒt△中，，．Ｒt△Ｒt△．　　．四边形是正方形．，；②过点，，如图．可以证明图中6与5位置的两个直角三角形全等，4与3位置的两个直角三角形全等，2与1位置的两个直角三角形也全等．所以将6放到5的位置，4放到3的位置，2放到１的位置，恰好拼接为正方形．（2）答：能．理由是：由上述的拼接过程可以看出：对于任意的两个正方形都可以拼接为一个正方形，而拼接出的这个正方形可以与第三个正方形再拼接为一个正方形，依次类推．由此可知：对于个任意的正方形，可以通过次拼接，得到一个正方形．3、在中，延长分别交于点．过Ｇ作于，过作于．，．8cm，\ncm．因此，矩形以每秒1cm的速度由开始向右移动到停止，和重叠部分的形状可分为下列三种情况：（1）当点由点运动到点的过程中，如图①所示，设与交于点，则重叠部分图形是，且．．（2）当点由点运动到点的过程中，如图②所示，重叠部分图形是直角梯形．．（3）当点由点运动到点的过程中，如图③所示，设与交于点，则重叠部分图形是五边形．4、解：（1）①如图1，当点与点重合时，，cm，所以与半圆所在的圆相切．此时点运动了2cm，所求运动时间为：\n．②如图2，当点运动到点时，过点作，垂足为．在Rt△中，，cm，则cm，即等于半圆的半径，所以与半圆所在的圆相切．此时点运动了8cm，所求运动时间为：图2③如图3，当点运动到的中点时，，cm，所以与半圆所在的圆相切．此时点运动了14cm，所求运动时间为：．④如图4，当点运动到点的右侧，且cm时，过点作直线，垂足为．在Rt△中，，则cm，即等于半圆所在的圆的半径，所以直线与半圆所在的圆相切．此时点运动了32cm，所求运动时间为：．因为半圆在运动中，它所在的圆与所在的直线相切只有上述①、③两种情形；与所在的直线相切只有上述②、④两种情形；与所在直线始终相交．所以只有当为，，，时，△的一边所在的直线与半圆所在圆相切．\n图4（2）当△的一边所在的直线与半圆所在的圆相切时，半圆与直径围成的区域与△三边围成的区域有重叠部分的只有如图2与图3所示的两种情形．①如图2，设与半圆的交点为，易知重叠部分是圆心角为，半径为6cm的扇形，所求重叠部分面积为：　（cm）．②如图3，设与半圆的交点为，连接，过点作，垂足为．则．在Rt△中，，cm，则cm，cm，cm．（cm）．又，（cm）．所求重叠部分面积为：（cm）．【励志故事】该低头时就低头被称为美国人之父的富兰克林，年轻时曾去拜访一位德高望重的老前辈。那时他年轻气盛，挺胸抬头迈着大步，一进门，他的头就狠狠地撞在门框上，疼得他一边不住地用手揉搓，一边看着比他的身子矮去一大截的门。出来迎接他的前辈看到他这副样子，笑笑说：“很痛吧！可是，这将是你今天访问我的最大收获。一个人要想平安无事地活在世上，就必须时刻记住：该低头时就低头。这也是我要教你的事情。”富兰克林把这次拜访得到的教导看成是一生最大的收获，并把它列为一生的生活准则之一。富兰克林从这一准则中受益终生，后来，他功勋卓越，成为一代伟人，他在他的一次谈话中说：“这一启发帮了我的大忙。”话外语：做人不可无骨气，但做事不可能总是仰着高贵的头。