历年初中数学中考规律试题集锦 答案分析 31页

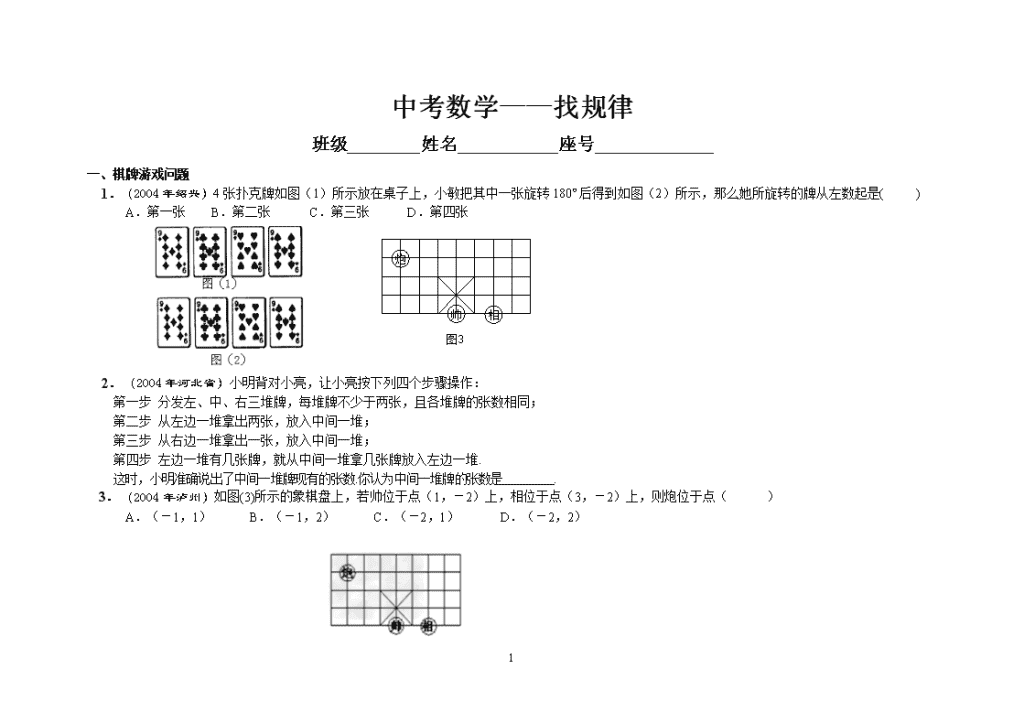
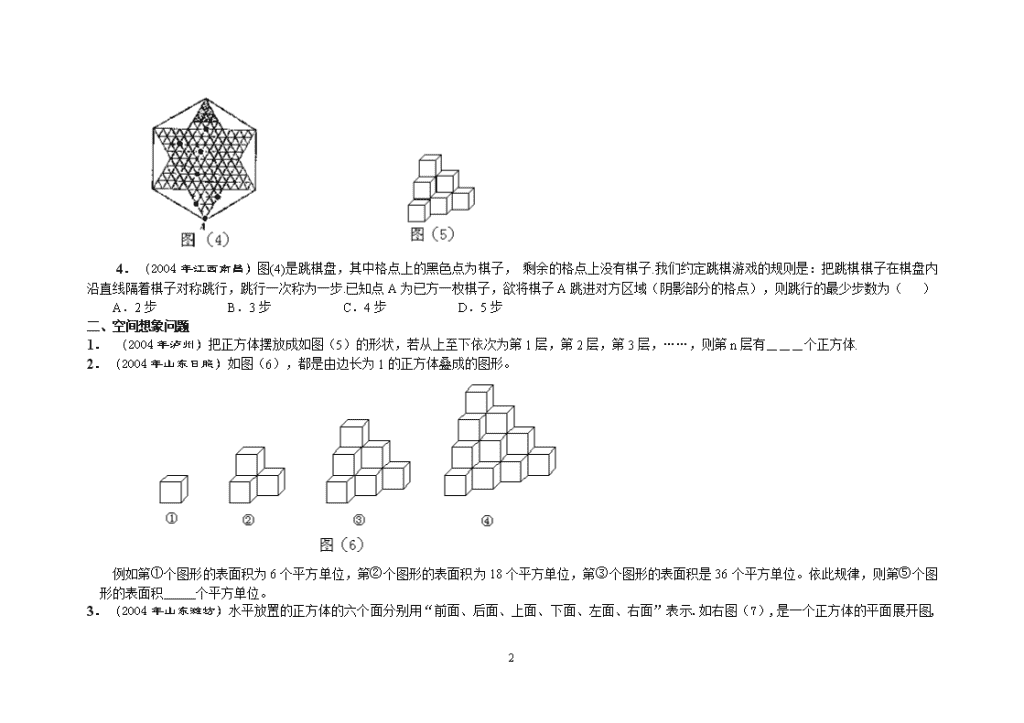
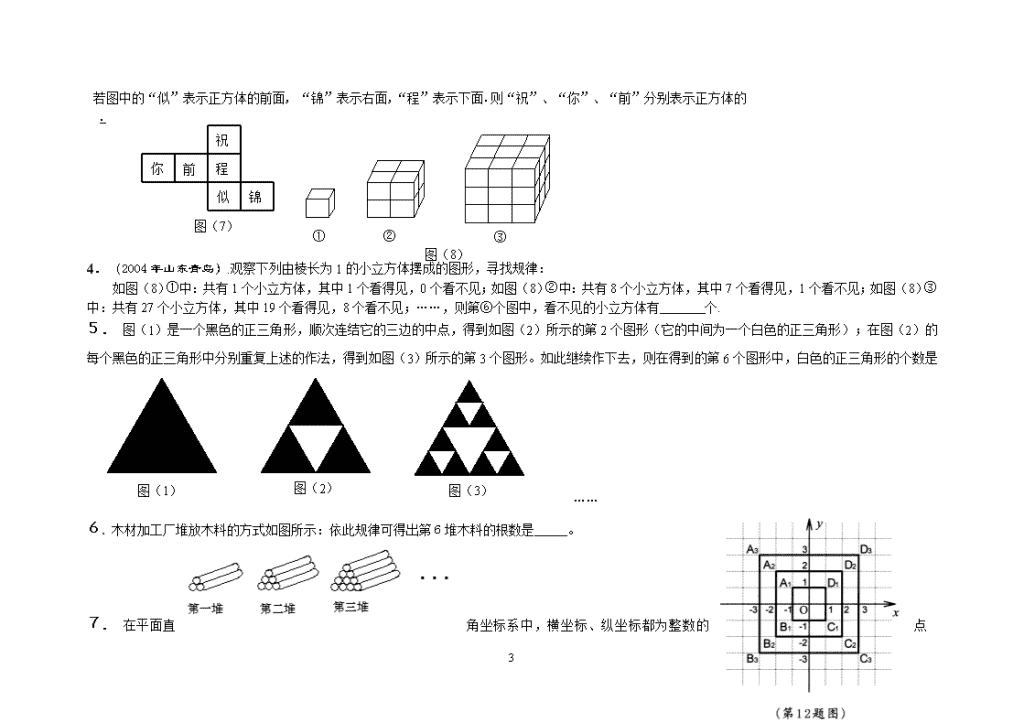
中考数学——找规律班级________姓名___________座号_____________一、棋牌游戏问题1．（2004年绍兴）4张扑克牌如图（1）所示放在桌子上，小敏把其中一张旋转180º后得到如图（2）所示，那么她所旋转的牌从左数起是()A．第一张　　B．第二张　　　C．第三张　　　D．第四张　2．（2004年河北省）小明背对小亮，让小亮按下列四个步骤操作：第一步分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；第二步从左边一堆拿出两张，放入中间一堆；第三步从右边一堆拿出一张，放入中间一堆；第四步左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是.3．（2004年泸州）如图(3)所示的象棋盘上，若帅位于点（1，－2）上，相位于点（3，－2）上，则炮位于点（　　　）　A．（－1，1）　B．（－1，2）C．（－2，1）　　　D．（－2，2）31\n4．（2004年江西南昌）图(4)是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子.我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿直线隔着棋子对称跳行，跳行一次称为一步.已知点A为已方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为（）A．2步B．3步C．4步D．5步二、空间想象问题1．（2004年泸州）把正方体摆放成如图（5）的形状，若从上至下依次为第1层，第2层，第3层，……，则第n层有＿＿＿个正方体.2．（2004年山东日照）如图（6），都是由边长为1的正方体叠成的图形。例如第①个图形的表面积为6个平方单位，第②个图形的表面积为18个平方单位，第③个图形的表面积是36个平方单位。依此规律，则第⑤个图形的表面积个平方单位。3．（2004年山东潍坊）水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”31\n表示.如右图（7）,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的.①②③图（8）程前你祝似锦图（7）4．（2004年山东青岛）.观察下列由棱长为1的小立方体摆成的图形，寻找规律：如图（8）①中：共有1个小立方体，其中1个看得见，0个看不见；如图（8）②中：共有8个小立方体，其中7个看得见，1个看不见；如图（8）③中：共有27个小立方体，其中19个看得见，8个看不见；……，则第⑥个图中，看不见的小立方体有个.５．图（1）是一个黑色的正三角形，顺次连结它的三边的中点，得到如图（2）所示的第2个图形（它的中间为一个白色的正三角形）；在图（2）的每个黑色的正三角形中分别重复上述的作法，得到如图（3）所示的第3个图形。如此继续作下去，则在得到的第6个图形中，白色的正三角形的个数是图（1）图（2）图（3）……６.木材加工厂堆放木料的方式如图所示：依此规律可得出第6堆木料的根数是。７．31\n在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你观察图中正方形A1B1C1D1、A2B2C2D2、A3B3C3D3……每个正方形四条边上的整点的个数，推算出正方形A10B10C10D10四条边上的整点共有　　　个.８、如图：是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当每边上摆20（即＝20）根时，需要的火柴棍总数为根。９.用火柴棒按如图的方式搭一行三角形，搭一个三角形需3支火柴棒，搭2个三角形需5支火柴棒，搭3个三角形需7支火柴棒，照这样的规律搭下去，搭n个三角形需要S支火柴棒，那么S关于n的函数关系式是(n为正整数)．10．如图，由等圆组成的一组图中，第1个图由1个圆组成，第2个图由7个圆组成，第3个图由19个圆组成，……，按照这样的规律排列下去，则第9个图形由__________个圆组成。……(第10题图)31\n11．一个正方体的每个面分别标有数字1，2，3，4，5，6．根据图1中该正方体A、B、C三种状态所显示的数字，可推出“？”处的数字是．12．下面是用棋子摆成的“上”字：第一个“上”字第二个“上”字第三个“上”字如果按照以上规律继续摆下去，那么通过观察，可以发现：（1）第四、第五个“上”字分别需用和枚棋子；（2分）（2）第n个“上”字需用枚棋子．（1分）13.将一张长方形的纸对折，如图5所示可得到一条折痕（图中虚线）．续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可以得到条折痕．如果对折n次，可以得到条折痕．14．下图是某同学在沙滩上用石于摆成的小房子．31\n观察图形的变化规律，写出第n个小房子用了块石子．15．为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：……①②③按照上面的规律，摆个“金鱼”需用火柴棒的根数为（）A．B．C．D．⑴⑵⑶⑷⑸……第17题图16.下面是按照一定规律画出的一列“树型”图：经观察可以发现：图⑵比图⑴多出2个“树枝”，图⑶比图⑵多出5个“树枝”，图⑷比图⑶多出10个“树枝”，照此规律，图⑺比图⑹多出_________个“树枝”．第16题图17．柜台上放着一堆罐头，它们摆放的形状见右图：第一层有听罐头，第二层有听罐头，第三层有听罐头，……根据这堆罐头排列的规律，第（为正整数）层31\n有听罐头（用含的式子表示）．18.按如下规律摆放三角形：则第（4）堆三角形的个数为_____________；第(n)堆三角形的个数为________________.（图4）19.一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分（如图4），则这串珠子被盒子遮住的部分有____颗.20．如图，图①，图②，图③，……是用围棋棋子摆成的一列具有一定规律的“山”字．则第个“山”字中的棋子个数是．……图①图②图③图④（第20题）31\n21．下列图案由边长相等的黑、白两色正方形按一定规律拼接而成。依次规律，第5个图案中白色正方形的个数为。…第1个第2个第3个第09题图22．用同样大小的正方形按下列规律摆放，将重叠部分涂上颜色，下面的图案中，第n个图案中正方形的个数是。第17题图n=1n=2n=3……23.如图，已知四边形ABCD是梯形（标注的数字为边长），按图中所示的规律，用2003个这样的梯形镶嵌而成的四边形的周长是______．24.在边长为l的正方形网格中，按下列方式得到“L”形图形第1个“L”形图形的周长是8，第2个“L”形图形的周长是12，则第n个“L”形图形的周长是.①②③31\n●●●●●●●●●●●●●●●●●●●●●●●●●●●●●25.观察下列图形,按规律填空:●………11+34+59+716+___…36+____26.用黑白两种颜色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一列图案：（1）第4个图案中有白色纸片张；（2）第n个图案中有白色纸片张.27．观察下表中三角形个数变化规律，填表并回答下面问题。问题：如果图中三角形的个数是102个，则图中应有___________条横截线。31\n28.用黑白两种颜色的正六边形地面砖按下图所示的规律拼成若干个图1.第1个图案中有白色地砖（   ）块,第2个图案中有白色地砖（   ）块,第3个图案中有白色地砖（   ）块2.第10个图案中有白色地砖（   ）块,.第n个图案中有白色地砖（   ）块图①图②图③…29．如图，下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），则第n个几何体中只有两个面涂色的小立方体共有________________个．（第14题）30.下列是三种化合物的结构式及分子式，如果按其规律，则后一种化合物的分子式应该是．14。31\n三、剪纸问题1．如图（9），把一个正方形三次对折后沿虚线剪下则得到的图形是（）2．小强拿了一张正方形的纸如图（10）①，沿虚线对折一次得图②，再对折一次得图③，然后用剪刀沿图③中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是（）3．如图（11），将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续下去，……，根据以上操作方法，请你填写下表：操作次数N12345…N…正方形的个数4710……四、对称问题1．仔细观察下列图案，如图（12），并按规律在横线上画出合适的图形。31\n2．分析图（14）①,②,④中阴影部分的分布规律，按此规律在图（14）③中画出其中的阴影部分.（2）在4×4的正方形网格中，请你用两种不同方法，分别在图①、图②中再将两个空白的小正方形涂黑，使每个图形中的涂黑部分连同整个正方形网格成为轴对称图形．3．在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如：鲁L80808　、鲁L22222、鲁L12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给以对称的美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。如果让你负责制作只以8和9开头且有五个数字的“数字对称”牌照，那么最多可制作（　　）A．2000个　　　B．1000个　　C．200个　　　D．100个4．已知n(n≥2)个点P1，P2，P3，…，Pn在同一平面内，且其中没有任何三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数，显然，S2=1，S3=3，S4=6，S5=10，…，由此推断，Sn=____________________31\n5.意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两上数的和。现以这组数中的各个数作为正方形的长度构造如下正方形：再分别依次从左到右取2个、3个、4个、5个,正方形拼成如下矩形并记为①、②、③、④.相应矩形的周长如下表所示：序号①②③④周长610xy仔细观察图形，上表中的x= ______ ，y= ______ ．若按此规律继续作长方形，则序号为⑧的长方形周长是 ______ ．五．1．观察图（13）的点阵图和相应的等式，探究其中的规律：（1）在④和⑤后面的横线上分别写出相应的等式；…………①1=12；②1+3=22；③1+2+5=32；④；⑤；图（13）31\n（2）通过猜想写出与第n个点阵相对应的等式＿＿＿＿＿＿＿＿＿＿＿＿＿＿.2．观察下列顺序排列的等式：9×0＋1＝1，9×1＋2＝11，9×2＋3＝21，9×3＋4＝31，9×4＋5＝41，……．猜想：第n个等式（n为正整数）应为____________________________．3.观察下列算式：，，，，，，，通过观察，用你所发现的规律确定的个位数字是（）A.2B.4C.6D.84．观察下列各式：1×3=+2×1，2×4=+2×2，31\n3×5=+2×3，请你将猜想到的规律用自然数n（n≥1）表示出来：。5.观察下列各式，你会发现什么规律？　　3×5＝42－1　　　　　　5×7＝62－1　　　　　　……11×13=122－1　　　请将你发现的规律用只含一个字母的表达式表示出来：　　　　　　　　　。6、观察下列不等式，猜想规律并填空：1+2>2×1×2；（）+（）>2××（－2）+3>2×（-2）×3；+>2××（－4）+(－3)>2×（－4）×(－3)；(－)+()>2××a+b>_____________(a≠b)7.．观察下面一列数：2，5，10，x，26，37，50，65，……，根据规律，其中x表示的数是。8．观察数列1,1,2,3,5,8,x,21,y,…,则2x-y=______________．9．观察下列等式：、、、……用含自然数n的等式表示这种规律为。10．已知：，，，…若（a、b为正整数），则a＋b＝。11．如果有2007名学生排成一列，按1、2、3、4、5、4、3、2、1、2、3、4、5、4、3、2、1……的规律报数，那么第2007名学生所报的数是．12．数字解密：第一个数是3=2＋1，第二个数是5=3＋2，第三个数是9=5＋4，第四个数是17=9＋8，……观察并猜想第六个数是。31\n13.观察下列等式：……………根据观察可得：_________.（n为正整数）14、古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为。15.观察下列等式9-1=816-4=1225-9=1636-16=20…………这些等式反映自然数间的某种规律，设n(n≥1)表示自然数，用关于n的等式表示这个规律为.16.观察下列等式：第一行3=4－1第二行5=9－4第三行7=16－9第四行9=25－16……按照上述规律，第n行的等式为____________17．有一列数，，，，，从第二个数开始，每一个数都等于与它前面那个数的倒数的差，若，则为（　　）Ａ．Ｂ．Ｃ．Ｄ．31\n18．观察下列等式：，，，，…请你把发现的规律用字母表示出来：．19．观察下列各式：……猜想：．20．观察下列等式：16－1=15；25－4=21；36－9=27；49－16=33；……用自然数n（其中）表示上面一系列等式所反映出来的规律是。21.按一定的规律排列的一列数依次为：┅┅，按此规律排列下去，这列数中的第7个数是.22．观察下列等式：、、、……31\n用含自然数n的等式表示这种规律为。23、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：输入输出24.观察下列各式，你会发现什么规律？　　3×5＝42－1　　　　　　5×7＝62－1　　11×13=122－1　　　………请将你发现的规律用只含一个字母的表达式表示出来：　　　　　　　　　。25.我国宋朝数学家杨辉在他的著作《祥解九章算法》中提出右表，此表揭示了（n为非负数）展开式的各项系数的规律。例如：，它只有一项，系数为1；，它有两项，系数分别为1，1；，它有三项，系数分别为1，2，1；，它有四项，系数分别为1，3，3，1；……根据以上规律，展开式共有五项，系数分别为。25．德国数学家莱布尼兹发现了下面的单位分数三角形（单位分数是分子为1，分母为正整数的分数）：第一行31\n第二行第三行第四行第五行……………根据前五行的规律，可以知道第六行的数依次是：　　　　　　．\历年初中数学找规律题（答案）一、棋牌游戏问题31\n1、A2、53、C4、B如图中红棋子所示，根据规则：①点A从右边通过3次轴对称后，位于阴影部分内；②点A从左边通过4次轴对称后，位于阴影部分内．所以跳行的最少步数为3步二、空间想象问题1、n(n+1)/2解析：等差数列第n层有正方体1+2+3+…+n=n(n+1)/2个．2、A结合图形，发现：第⑤个图形的表面积是（1+2+3+4+5）×6=90．故选A．3、后面、上面、左面4、125解析：n=1时，看见的小立方体的个数为1；看不见的小立方体的个数为0个；n=2时，看见的小立方体的个数为2×2×2=8个；看不见的小立方体的个数为1个；n=3时，看见的小立方体的个数为3×3×3=27个；看不见的小立方体的个数为2×2×2=8=8个；n=4时，看见的小立方体的个数为4×4×4=64个；看不见的小立方体的个数为3×3×3=27个；…n=6时，看见的小立方体的个数为6×6×6=216个；看不见的小立方体的个数为5×5×5=125个；故应填125个．5、121解析：设白三角形x个，黑三角形y个，则：n=1时，x=0，y=1；n=2时，x=0+1=1，y=3；（1个白三角形能分割出3个黑三角形）n=3时，x=3+1=4，y=9；（3个黑三角形又被分割成3*3=9个黑三角形）31\nn=4时，x=4+9=13，y=27；（9个黑三角形又被分割成9*3=27个黑三角形）......n=5时，x=13+27=40，y=81；当n=6时，x=40+81=121．所以白的正三角形个数为：121．6、28解析:设木料根数为s．则第一堆s=1+2=3；第二堆s=1+2+3=6；第三堆s=1+2+3+4=10；…；第n堆s=1+2+3+…+（n+1）=[(n+1)(n+2)]/2．(若公差d=1时：Sn=(a1+an)n/2,n为一共有几项)当n=6时，s=[(6+1)(6+2)]/2=28．故选C．7、80解析：第1个正方形上的整点个数是8；第2个正方形上的整点个数是16；第3个正方形上的整点个数是24；所以 第n个正方形上的整点个数是：4+4（2n-1）=8n，第10个正方形上的整点个数是：80个。n               整点数                       分解1                   8                        1×82                  16                        2×83                  24                        3×84                  32                        4×85                  40                        5×8所以整点数为n×8。正方形A10B10C10D10四条边上的整点共有80个。8、630解析：n=1时，有1个三角形，需要火柴的根数为：3×1；31\nn=2时，有3个三角形，需要火柴的根数为：3×（1+2）；n=3时，有6个三角形，需要火柴的根数为：3×（1+2+3）；…；n=20时，需要火柴的根数为：3×（1+2+3+4+…+20）=630．故答案为：630．9、s=2n+110、217解析：观察分析可得：第1个图形有1个圆，第2个图由1+6=7个圆组成，第3个图由7+2×6=19…，第9个图形由1+6+12+18+24+30+36+42+48=217个圆．11、612、（1）18、22（2）S=4n+2第1个“上”字用6个棋子，第2个“上”字用10个棋子，比第1个多用了4个；第3个“上”字用14个棋子，比第2个多用了4个．…每一个比上一个多用4个．所以第n个“上”字需用4n+2个．故答案为：S=4n+2．13、（1）15条（2）第1次对折，折痕为1；（2-1=1）第2次对折，折痕为1+2；（4-1=1）第3次对折，折痕为；（8-1=1）第n次对折，折痕为14、n=-4解析：5=-431\n12=-421=-432=-4所以第n个=-415、A16、37由题意，图（2）比图（1）多出2个“树枝”，图（3）比图（2）多出5个“树枝”，图（4）比图（3）多出10个“树枝”，照此规律，an+1-an=n2+1故答案为：an+1-an=62+1=3717、（n+1）（n+2)18、3n+2分析：此题首先注意正确数出第一个图形中三角形的个数，然后进一步发现后边的图形比前边的图形多几个．从而推广到一般．解：首先观察第一个图形中有5个．后边的每一个图形都比前边的图形多3个．则第n堆中三角形的个数有5+3（n-1）=3n+2．点评：此题考查了平面图形，主要培养学生的观察能力和空间想象能力19、2420、5n+221、5n+3解析：第n个图形中共有黑色正方形n个,共有正方形（包含黑色和白色）6n+3,白色为6n+3-n=5n+322、4n-1解析：根据题意分析可得：第1个图案中正方形的个数4×1-1=3个，第2个图案中正方形的个数4×2-1=7个，…，第n个图案中正方形的个数4×n-1个23、601131\n解析：用2003个这样的梯形镶嵌而成的四边形为一个梯形，两腰为1，上底为1001×3+1=3004．下底为1001×3+2=3005；故其周长为3005+3004+2=6011．答案6011．24、4n+4解析：观察可得：第1个“L”形图形的周长8，有4×1+4=8．第2个“L”形图形的周长12，有4×2+4=12．第3个“L”形图形的周长12，有4×3+4=16．…第n个“L”形图形的周长4×n+4=4n+4．25、9、13解析：第5个图形中，是16+9，第7个图形中，是36+1326、13、3n+1根据分析可得图中有白色纸片个数的通项公式：1+3n；所以第4个图中有白色纸片：1+3×4=13（张）；答：第4个图中有白色纸片13张．27、16解析：1）没有横线的时候，只有6个三角形；有一条横线的时候，有6×2个三角形；有2条横线的时候，有6×3个三角形；∴当横截线条数为n条时应有6×（n+1）个三角形．（2）让6×（n+1）=102，解得n=16．28、4n+2解析：观察可知：除第一个以外，每增加一个黑色地板砖，相应的白地板砖就增加四个，∵第n个图案中有白色地面砖的块数是一个“以6为首项，公差是4的等差数列的第n项”，∴第n个图案中有白色地面砖的块数是4n+2，31\n29.8n-4解析：观察图形可知：图①中，两面涂色的小立方体共有4个；图②中，两面涂色的小立方体共有12个；图③中，两面涂色的小立方体共有20个．4，12，20都是4的倍数，可分别写成4×1，4×3，4×5的形式，因此，第n个几何体中只有2个面涂色的小立方体共有的块数为：4（2n-1）=8n-4，故答案为8n-4．30、C4H10三、剪纸问题1、C2、D3、13,16,3n+1四、对称问题1、E的对称图形2、略3、C解析：在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如：鲁L80808　、鲁L22222、鲁L12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给以对称的美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。如果让你负责制作只以8和9开头且有五个数字的“数字对称”牌照，那么最多可制作4、5、16；26；178解析：31\n解：由分析知：第1个长方形的周长为6=（1+2）×2；第2个长方形的周长为10=（2+3）×2；第3个长方形的周长为16=（3+5）×2；第4个长方形的周长为26=（5+8）×2；第5个长方形的周长为42=（8+13）×2；第6个长方形的周长为68=（13+21）×2；第7个长方形的周长为110=（21+34）×2；第8个长方形的周长为178=（34+55）×2．故，答案为：16；26；178．五、1、略2、9（n-1）+n=10n-93、D4、5、2n-1）（2n+1）=4n2-1（n≥2，n为自然数）解：左边是两相邻的奇数之积，右边是一个偶数的平方减1，由此猜出本题的规律是：（2n-1）（2n+1）=4n2-1（n≥2，n为自然数）。6、2ab7、178、131,1,2,3,5,8,(13）,(21) 1+1=2 2+3=5 3+5=8 所以:5+8=138+13=219、10、10911、312、65看每个式子的第一个加数,后面的都是前面的2倍减1看每个式子的第二个加数,后面都是前面的2倍.所以第五个数是17+16=33第六个数是33+32=6531\n13、根据等式左边的奇数的规律，我们可以表示出第n个数为2n-1，那么所求的1+3+5+…+2n-1，实际上是求n个奇数的和，那么等式的右边就应该等于．故答案为14、47解析：第1个三角形数是1；第2个三角形数是3=1+2；第3个三角形数是6=1+2+3；第4个三角形数是10=1+2+3+4；.第n个三角形数是1+2+3+4+.+n=n(n+1)/2.则第24个三角形与第22个三角形的差为24(24+1)/2-22(22+1)/2=12×25-11×23=300-253=47.15、(n+1)²-(n-1)²=4n解析：即3²-1²=4×24²-2²=4×35²-3²=4×4所以(n+1)²-(n-1)²=4n证明(n+1)²-(n-1)²=[(n+1)+(n-1)][(n+1)-(n-1)]=(2n)×2=4n16、2n+1=第一行1×2+1=31\n第二行2×2+1=第三行3×2+1=第四行4×2+1=…第n行2n+1=．17、解：∵a1=2，∴a2=1-  =  ，a3=1-2=-1，a4=1-（-1）=2，a5=1-  =    ，…依次类推，每3个数为一组进行循环18、19、略20、(n+3)2-n2=6n+931\n21、2=1平方+1 3=2平方-1 10=3平方+1 15=4平方-1 26=5平方+1 35=6平方-1 7平方+1=50第7个数字为5031\n古今名言敏而好学，不耻下问——孔子业精于勤，荒于嬉；行成于思，毁于随——韩愈兴于《诗》，立于礼，成于乐——孔子己所不欲，勿施于人——孔子读书破万卷，下笔如有神——杜甫读书有三到，谓心到，眼到，口到——朱熹立身以立学为先，立学以读书为本——欧阳修读万卷书，行万里路——刘彝黑发不知勤学早，白首方悔读书迟——颜真卿书卷多情似故人，晨昏忧乐每相亲——于谦书犹药也，善读之可以医愚——刘向莫等闲，白了少年头，空悲切——岳飞发奋识遍天下字，立志读尽人间书——苏轼鸟欲高飞先振翅，人求上进先读书——李苦禅立志宜思真品格，读书须尽苦功夫——阮元非淡泊无以明志，非宁静无以致远——诸葛亮熟读唐诗三百首，不会作诗也会吟——孙洙《唐诗三百首序》书到用时方恨少，事非经过不知难——陆游问渠那得清如许，为有源头活水来——朱熹旧书不厌百回读，熟读精思子自知——苏轼书痴者文必工，艺痴者技必良——蒲松龄31\n声明访问者可将本资料提供的内容用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律的规定，不得侵犯本文档及相关权利人的合法权利。谢谢合作！31