决战新高考2009年高考模拟试卷 23页

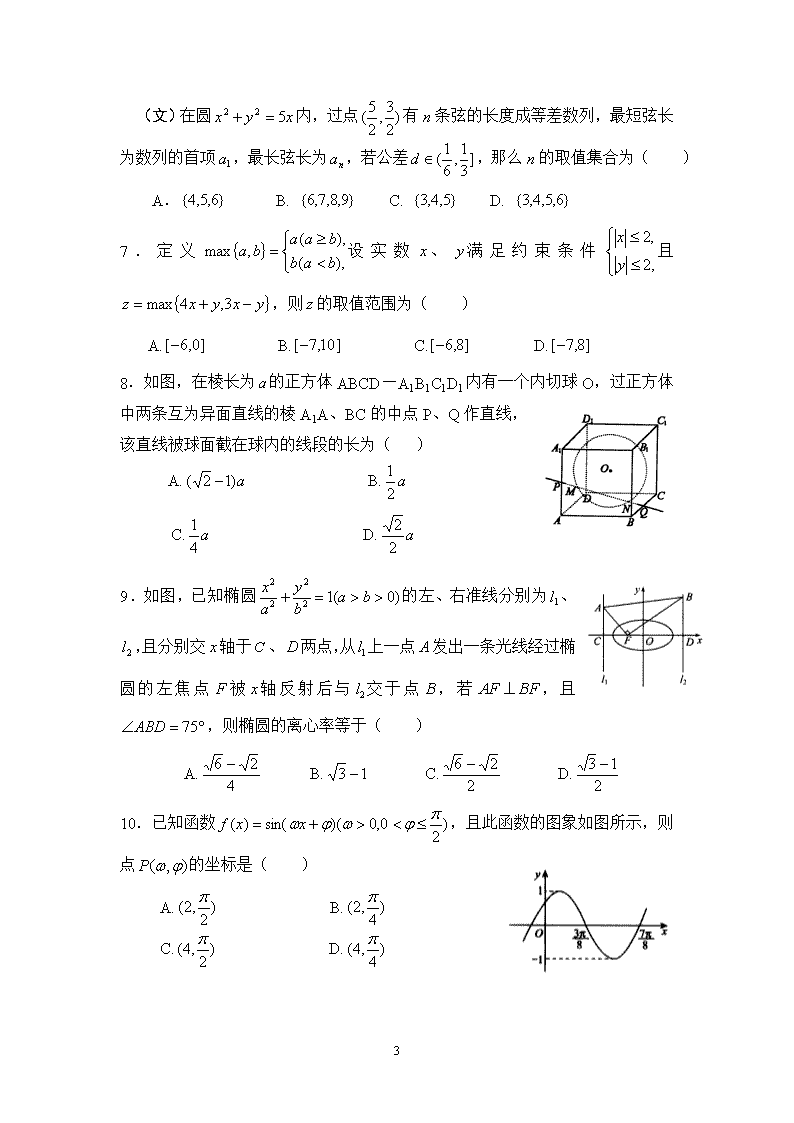
决战新高考——2009年高考模拟试卷数学湖北省襄樊市第一中学特级教师王勇（441000）【命题导航】本套试卷在命制的时候认真研读了最新高考《考试大纲》及有关省市《考试说明》，详细地研究了近几年的高考试题，对过去几年高考中对各章的考查进行了详细统计，在此基础上确定了命题范围与题目的分布情况.因此本试卷注重了对基础知识的考查，既全面又突出重点，试卷在创新方面较为突出，整卷基本上按照由易到难的顺序编排，每种题型也按照由易到难的顺序进行编排，充分发挥了各种题型的考查功能.试卷模式与2008年全国卷完全相符，在试题的具体设计上，也有诸多创新之处，展示了命题人对高考命题的一些最新研究成果，如第1题、第5题、第7题是信息迁移题，着重考查学生阅读理解能力和分析问题、解决问题的能力.第3题、第6题、第12题、第15题、第17题、第21题、第22题等是交汇综合题，着重考查学生综合运用数学知识的能力.第4题（文）、第18题用现实生活中身边的事例命题，富有时代和生活气息.第5题、第7题、第11题、第16题、第21题、第22题是探索开放题，立意新颖，构思精巧，极富思考性和挑战性.本试卷对新教材新增内容平面向量、导数、概率与统计、线性规划等内容考查的力度相当大，如第3题（理）、第4题、第7题、第15题、第17题、第18题、第20题、第22题等.对常用的数学思想方法，如函数和方程、数形结合、分类讨论、转化与化归等考查的也相当充分，同时兼顾了对学生数学思维品质和个性品质的考查.总之这套试卷较好地代表了高考命题的趋势及方向，真正体现了试题的选拔功能.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合，，定义23\n，则集合的所有真子集的个数为（）A.32B.31C.30D.以上都不对2．设函数的反函数为，且，则的值为（）A.B.C.1D.23．（理）若，则下列各结论中正确的是（）A.B.C.D.（文）若函数且，则、、的大小关系是（）A.B.C.D.4．（理）设函数在处连续，且，则等于（）A.B.0C.1D.2（文）某工厂有甲、乙、丙、丁四类产品的数量成等比数列，共计3000件，现要用分层抽样的方法从中抽取150件进行质量检测，其中乙、丁两类产品抽取的总数为100件，则甲类产品总共有（）A.100件B.200件C.300件D.400件5．如果一条直线与一个平面平行，那么，称此直线与平面构成一个“平行线面对”，在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面对”的个数是（）A.24B.36C.48D.606．（理）命题不等式的解集为；命题在中，是成立的必要不充分条件.则（）A.真假B.且为真C.或为假D.假真23\n（文）在圆内，过点有n条弦的长度成等差数列，最短弦长为数列的首项，最长弦长为，若公差，那么n的取值集合为（）A．B.C.D.7．定义设实数、满足约束条件且，则的取值范围为（）A.B.C.D.8．如图，在棱长为的正方体ABCD—A1B1C1D1内有一个内切球O，过正方体中两条互为异面直线的棱A1A、BC的中点P、Q作直线，该直线被球面截在球内的线段的长为（）A.B.C.D.9．如图，已知椭圆的左、右准线分别为、，且分别交轴于、两点，从上一点发出一条光线经过椭圆的左焦点被轴反射后与交于点，若，且，则椭圆的离心率等于（）A.B.C.D.10．已知函数，且此函数的图象如图所示，则点的坐标是（）A.B.C.D.23\n11．已知、分别是双曲线的左、右焦点，为双曲线上一点，过作的平分线的垂线，垂足为.则点的轨迹为（）A.椭圆B.双曲线C.圆D.抛物线12．数列中，N*)，数列中，N*)，已知点则向量的坐标为（）A.B.C.D.第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.13．若,则=______________.14．已知不等式对任意正实数恒成立，则正实数的最小值为___________________.15．（理）设，、R，将一个骰子连续抛掷两次，第一次得到的点数为，第二次得到的点数为，则使复数为纯虚数的概率为__________.（文）在的展开式中任取一项，则所取项为有理项的概率为_________.16．如图，在正方体中，给出下列四个命题：①点在直线上运动时，三棱锥23\n的体积不变；②点在直线上运动时，直线与平面所成角的大小不变；③点在直线上运动时，二面角的大小不变；④点是平面上到点和距离相等的点，则点的轨迹是过点的直线.其中真命题的编号是______________.（写出所有真命题的编号）三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)(理)已知向量，，，向量与的夹角为，向量与的夹角为，且.若中，角、、的对边分别为、、，且角.（1）求角的大小；（2）若的外接圆半径为，试求的取值范围.（文）、、为的三内角，且其对边分别为、、，若，，且.（1）求角的大小；（2）若的面积，求的值.18．（本小题满分12分）（理）现有分别写有数字1，2，3，4，5的5张白色卡片、5张黄色卡片、5张红色卡片.每次试验抽一张卡片，并定义随机变量，如下：若是白色，则，若是黄色，则，若是红色，则，若卡片数字是，则.（1）求概率；23\n（2）求数学期望.（文）现有分别写有数字1，2，3，4，5的5张白色卡片、5张黄色卡片、5张红色卡片.每次试验抽一张卡片，对作如下约定：若取到一张写有数字为的白色卡片，则得分，若取到一张写有数字为的黄色卡片，则得分，若取到一张写有数字为的红色卡片，则得分.（1）求得分为3分的概率；（2）求得分大于3分的概率.19．（本小题满分12分）如图，在三棱锥中，是边长为4的正三角形，平面平面，，、分别为、的中点.（1）求证：；（2）求二面角的大小；（3）求点到平面的距离.20．（本小题满分12分）（理）已知函数R).（1）若在时取得极值，求的值；（2）求的单调区间；（3）求证：当时，.（文）已知函数R)的图象与直线相切于点，且函数在处取得极值.（1）求的解析式；（2）求的极值；（3）当时，求的最大值.21．（本小题满分12分）如图，已知点，点在轴上，点在轴的正半轴上，点在直线上，且满足23\n.（1）当点在轴上移动时，求点的轨迹；（2）过定点作直线交轨迹于、两点，是点关于坐标原点的对称点，求证：.（3）（只理科做）在（2）中，是否存在垂直于轴的直线被以为直径的圆截得的弦长恒为定值？若存在，求出直线的方程；若不存在，请说明理由.22．（本小题满分14分）（理）已知函数的反函数为，设在点N*)处的切线在轴上的截距为，数列满足：N*).（1）求数列的通项公式；（2）在数列中，仅当时，取最小值，求的取值范围；（3）令函数，数列满足：N*)，求证：对于一切的正整数，都满足：.（文）已知函数的反函数为，数列满足：N*).（1）求数列的通项公式；（2）设函数在点N*)处的切线在轴上的截距为，求数列的通项公式；（3）在数列中，仅当时，取最大值，求的取值范围.23\n考后分析相关事宜测试学校难度系数平均分最高分130分以上人数百分比120~130分人数百分比110~120分人数百分比100~110分人数百分比襄樊市一中0.571141459.8%8.8%10.3%14.8%【测试评价与备考策略】从测试结果来看，主要存在以下问题：①学生面对新颖的试题不知道如何入手，一时找不到解题的突破口，思维不能快速进入解题状态.如第5题、第7题、第9题、第12题、第15题、第21题、第22题等.②学生构造模型，利用模型的能力不够强，这需要在平时的解题训练中，要有意识地记忆、理解模型的有效价值，这对于不断提升学生的分析问题和解决问题的能力是大有裨益的.如第3题、第8题、第16题、第21题、第22题等.③学生画图不准确，读图时的信息翻译常有差错，抓不住问题的关键点.如第8题、第10题、第11题、第16题、第21题等.④学生对一些基本概念模糊，基本的运算不正确及基本的方法不熟练而失分的现象比较严重.如第1题、第9题、第12题、第15题、第21题、第22题等.针对以上情况，建议考生先抓重点复习，平时多训练客观题的解题速度、主观题的踩分点，要针对自己的弱项狠下工夫，多回头看看自己以前做过的题，进行整理归纳，多问自己几个为什么，为什么错，剖析出错的原因，还有有些题目碰巧做对了，但不是真正凭知识和能力做出来的，而是凭感觉，这些都需要自己再加强，从根本上提高自己的解题能力，高考靠的是实力而不是碰运气.数学参考答案与提示1．B由所定义的运算可知，的所有真子集的个数为.故选B.【点评】本题是一道信息迁移题，弄懂的本质含义并记住当时，的子集、真子集、非空真子集的个数分别为、、是求解本题的关键.2．A由，由分段函数解析式知只能，于是.故选A.23\n【点评】本题考查分段函数和反函数的基础知识，求出的值是解决问题的突破口.3．（理）D，当时，在内为单调减函数.又，，.故选D.【点评】本题利用导数研究函数的单调性再结合均值不等式求解.（文）B、、可看作函数图象上的点与原点所确定的直线的斜率，结合函数的图象及可知.故选B.【点评】本题抓住、、的几何意义再结合函数图象求解.4．（理）B函数在处连续，且，一定含有因式，于是.故选B.【点评】根据函数在一点连续的定义，有，即求函数在时的极限值，就是求在处的函数值.（文）B设甲、乙、丙、丁四类产品分别抽取件进行检测，由于四类产品的数量成等比数列且是分层抽样，所以也成等比数列，设此等比数列的公比为，由即解得即甲类产品抽取10件，则甲类产品的数量为（件）.故选B.【点评】注意到分层抽样的特点，四类产品的数量成等比数列，则抽取的数量也成等比数列，可由等比数列的知识先求出甲类产品抽取的数量，那么甲类产品的数量便迎刃而解.5．C当平面取正方体的表面时，与一个表面平行的直线有：与其相对的表面的四条边和两条对角线共6条，这样的“平行线面对”23\n有36个；当平面取正方体的对角面时，与一个对角面平行的直线有两条，这样的“平行线面对”有12个，故共有36+12=48（个）.故选C.【点评】立体几何中的排列组合计数问题，是高考中得分率极低的一道题，解决这类问题的关键，一是对立体几何中的有关概念和性质要熟悉掌握，二是一般按先分类再分步计数.分类时，要找到合理的分类标准，既要注意类与类之间的对称性和互换性，又要注意避免重复计数.如本题中，将正方体中的面分为表面和对角面两类，然后根据各类情况再分步计数.6．（理）A解不等式可知为真；对于命题进行三角变换，降次切入，由.由此可见是成立的充要条件，命题为假命题.故选A.【点评】本题以命题真假的判断为载体，考查解不等式和三角形中的三角变换，值得考生回味.（文）A由题意得，，，，，，，，.故选A.【点评】本题首先必须明确过圆内一点的最长弦和最短弦各自的特点,在此基础上结合数列和不等式知识方可圆满解决.7．B，直线将约束条件所确定的平面区域分为两部分.如图，令，点在四边形上及其内部，求得；令，点在四边形上及其内部（除边），求得.综上可知，23\n的取值范围为.故选B.【点评】表面上看约束条件和目标函数都是静态的，实际上二者都是动态变化的，目标函数是还是并没有明确确定下来，直线又将原可行域分为两部分.本题看似风平浪静，实际暗藏玄机，化动为静，在静态状态下，从容破解问题.8．D如图，连结PO交对棱于R，则R为对棱的中点，取MN的中点H，则.从而OH//RQ，且.故，.故选D.【点评】本题着重考查空间想象能力和运算能力，添加适当的辅助线并结合平面几何知识可圆满解决.9．C由光学知识易知、均为等腰直角三角形，，，，即，，，.故选C.【点评】离心率是圆锥曲线的一个重要特征量，是高考“经久不衰”23\n的重点和热点内容，必须高度重视.本题以椭圆为载体，巧妙地将光的反射融于其中，对平面几何及解析几何的考查均非常深刻，对计算能力要求较高，极富思考性和挑战性，具有较好的区分和选拔功能.10．B由图象可得函数的周期，得.将代入可得，由可得.点的坐标是.故选B.【点评】本题考查了由三角函数的图象求三角函数解析式的方法，体现了抓住图象信息解题的能力要求.解题中对的求解要注意特征点的选择与代入.11．C如图，过作的平分线的垂线，垂足为，交的延长线于，则，而.连结，则是的中位线，.点的轨迹是以为圆心，为半径的圆.故选C.【点评】本题考查双曲线的第一定义及平面几何的有关性质，是一道小巧玲珑、新颖别致的好题，充当着“小题把关”的重要角色.12．B由得，所以数列是等差数列.又，，可得该数列的公差.又由得，所以数列是等比数列.又，，可得该数列的公比.由题意，，所以，其中.，而是以为首项，公比为的等比数列，是以23\n为首项，公比为的等比数列..于是所求和向量的坐标为.故选B.【点评】本题考查等差中项与等比中项、等差数列通项公式、等比数列前项和公式以及向量的坐标运算等知识，综合性强、难度较大，是一道优秀的创新试题.13．0令，则；令，则，.【点评】本题考查二项展开式的系数和的问题，解决这类问题的有效方法是“赋值法”，即对赋予特殊值即可.要注意的是所求的和不是所有的系数和，而是少了一个“”.14．4，，由题意有，解得.【点评】不等式对任意正实数恒成立，这就是解题的切入点和突破口.15．（理），要使为纯虚数需，又抛掷一个骰子两次共有36种不同的结果，而两次点数相同的只含6种，故所求概率为.23\n【点评】本题将复数与概率交汇考查，魅力四射、回味无穷.（文）因为展开后展开式一共12项，其通项公式为，其中只有第4项和第10项是有理项，故所求概率为.【点评】本题将二项式定理与概率交汇考查，新颖别致、匠心独运.16．①③④平面，当点在直线上运动时，点到平面的距离不变，三棱锥的体积不变，所以命题①正确；当点在直线上运动时，点到平面的距离不变，但的长度变化，直线与平面所成的角的大小变化，所以命题②不正确；当点在直线上运动时，点到平面的距离不变且点到直线的距离也不变，二面角的大小不变，所以命题③正确；点到点和点的距离相等，和在平面上的射影也相等，点在平面上的射影为点，点的轨迹是直线，所以命题④正确.【点评】据统计，填空题是每年高考得分率偏低的题型，主要原因是填空题要求结果绝对精确.近年来，高考命题者又把填空题当作创新改革题型的“试验田”，相继推出一些题意新颖，构思精巧，具有相当深度和明确导向的创新题型，这样，越发加大了填空题的难度，致使部分学生谈“空”色变.本题给出多个命题，要答题者对每个备选命题判断其真伪性，填写满足要求的命题序号.这是近年出现的新题型，属于选择题中的多选题，排除了“唯一性”中“猜”的成份，多个结论的开放加大了问题的难度，必须对每个备选命题逐一研究其真伪性，才能探索出正确答案，这类题型考查容量大，多选或少选一个全题皆错.17．（理）（1），，，，，，同理，，而，，，23\n又，，，，根据条件，可得，.（6分）（2）由正弦定理可得：，.再由余弦定理可得：，代入数据并整理可得：，根据不等式可得，，，又，的取值范围为.（12分）【点评】本题由一道常见的题目巧妙改编而成，考查平面向量与三角函数的交汇，其中正弦定理、余弦定理、均值不等式等的参与，给本题增色添彩，堪称一道优秀的创新题.（文）（1），，且，，即，又，.（6分）（2），.又由余弦定理得：，.（12分）【点评】是一道用平面向量“包装”的三角题，考查的知识点多，但难易适中，能有效稳定文科考生的考试情绪，吊起考生的解题胃口.18．（理）（1）满足的数对有三种.而表示取到一张写有数字3的白色卡片，此时概率，同理数对对应的概率为，数对对应的概率为..（6分）（2）的所有可能取值为1,2,3,4,5,6,7.（8分）23\n于是的分布列为：1234567（10分）=4.（12分）【点评】本题考查互斥事件的概率加法公式，重点考查随机变量的分布列与期望，读懂题目所给的定义是求解的关键.（文）（1）得分为3分的情况有如下三种：取到一张标有数字3的白色卡片；取到一张标有数字2的黄色卡片；取到一张标有数字1的红色卡片.于是得分为3分的概率.（6分）（2）得分为2分的情况有如下两种：取到一张标有数字2的白色卡片；取到一张标有数字1的黄色卡片，得分为2分的概率.又得分为1分的情况只有一种：取到一张标有数字1的白色卡片，得分为1分的概率.得分大于3分的概率.（12分）【点评】本题考查互斥事件的概率加法公式，其中第（2）问所用的思想方法“正难则反”值得充分借鉴和回味.读懂题目所给的约定是求解的关键.19．（1）取的中点，连结、.，，且.又平面平面，平面平面，平面，又平面，.建立如图所示的空间直角坐标系，则，，，，，，，，，.（4分）23\n（2）由（1）得，.设为平面的一个法向量，则取，则，，.又为平面的一个法向量，.二面角的大小为.（8分）（3）由（1）、（2）得，为平面的一个法向量，点到平面的距离.（12分）【点评】立体几何是每年高考必考的一道解答题，证明异面直线垂直，求二面角及点到平面的距离都是很重要的考点.本题第（1）问用传统方法证明很简单，但对解决第（2）、（3）问的台阶和铺垫作用不明显，故第（1）问也采用了向量证法.高考中的立体几何题，一般说来既可用传统方法解决，也可用向量方法征服，请同学们结合具体题目和所给图形灵活选用.20．（理）（1），是一个极值点，，.（2分）此时.的定义域是，当时，；当时，.当时，是的极小值点，.（4分）（2）当时，的单调递增区间为.（6分）23\n当时，，令有，函数的单调递增区间为；令有，函数的单调递减区间为.（8分）（3）设，，当时，，在上是增函数，，当时，（12分）【点评】考查导数在研究函数性质、证明不等式等方面的应用，充分体现了导数的工具作用.（文）（1），的图象与直线相切于点，①又在处取得极值，.②（2分）由①、②解得.（4分）（2），令得，.列表如下：0(0,4)4+0－0+↗2↘↗从而当时，的极大值为2；当时，的极小值为.(8分)23\n（3）由（2）知是极大值，在内函数单调递增，并且可验证，据已知条件知，当时，的最大值是；当时，的最大值是.（12分）【点评】考查导数在研究函数性质方面的应用，其中导数的几何意义、分类讨论思想的应用都是高考的重点和热点.21．（理）（1）设，，.，，且，，，..动点的轨迹是以为顶点，以为焦点的抛物线（除去顶点）.（4分）（2）如图，依题意，设直线的方程为，，，则两点的坐标满足方程组消去并整理，得，，.设直线和的斜率分别为、，则23\n.，即.又，，.（8分）（3）假设存在满足条件的直线，其方程为，的中点为，与以为直径的圆相交于点、，的中点为，则，点的坐标为.，=，.令，得，此时，，当，即时，（定值）.综上可知，当时，满足条件的直线存在，其方程为；当时，满足条件的直线不存在.（12分）【点评】本题考查解析几何中轨迹方程的求法、直线与圆锥曲线的位置关系等，其中第（3）问设计为一个探究性的问题，加大了题目难度，有较好的区分和选拔功能.23\n（文）（1）设，，.，，且，，，..动点的轨迹是以为顶点，以为焦点的抛物线（除去顶点）.（6分）（2）如图，依题意，设直线的方程为，，，则两点的坐标满足方程组消去并整理，得，，.设直线和的斜率分别为、，则.，23\n即.又，，.（12分）【点评】本题考查解析几何中轨迹方程的求法、直线与圆锥曲线的位置关系等，对文科考生而言，难易适中，有望破解.22．（理）（1），函数的反函数为.则，得，即，数列是以2为首项、1为公差的等差数列，故.（4分）（2）又，函数在点N*)处的切线方程为：，令，得.，仅当时取得最小值，只需，解得.故的取值范围为.（9分）（3），故，又，故，则，即.=.又23\n，故.（14分）【点评】本题是函数、数列、导数等的大型综合题，衔接自然，叙述流畅，毫无拼凑的痕迹，情景新颖，具有较好的区分度，入口较宽.要求学生具有一定的审题、读题能力，一定的等价变形能力，要求学生具有较高的数学素养和数学灵气.（文）（1），函数的反函数为.则，得，即，数列是以2为首项、1为公差的等差数列，故.（4分）（2），，即在点N*)处切线的斜率，切线方程为，令，得.（9分）（3），仅当时取最大值，只需，解得.故的取值范围为.（14分）【点评】本题是函数、数列、导数等的大型综合题，衔接自然，叙述流畅，毫无拼凑的痕迹，情景新颖，具有较好的区分度，入口较宽.要求学生具有一定的审题、读题能力，一定的等价变形能力，要求学生具有较高的数学素养和数学灵气.23