高考数学复习点拨 高考中的定积分_1 2页

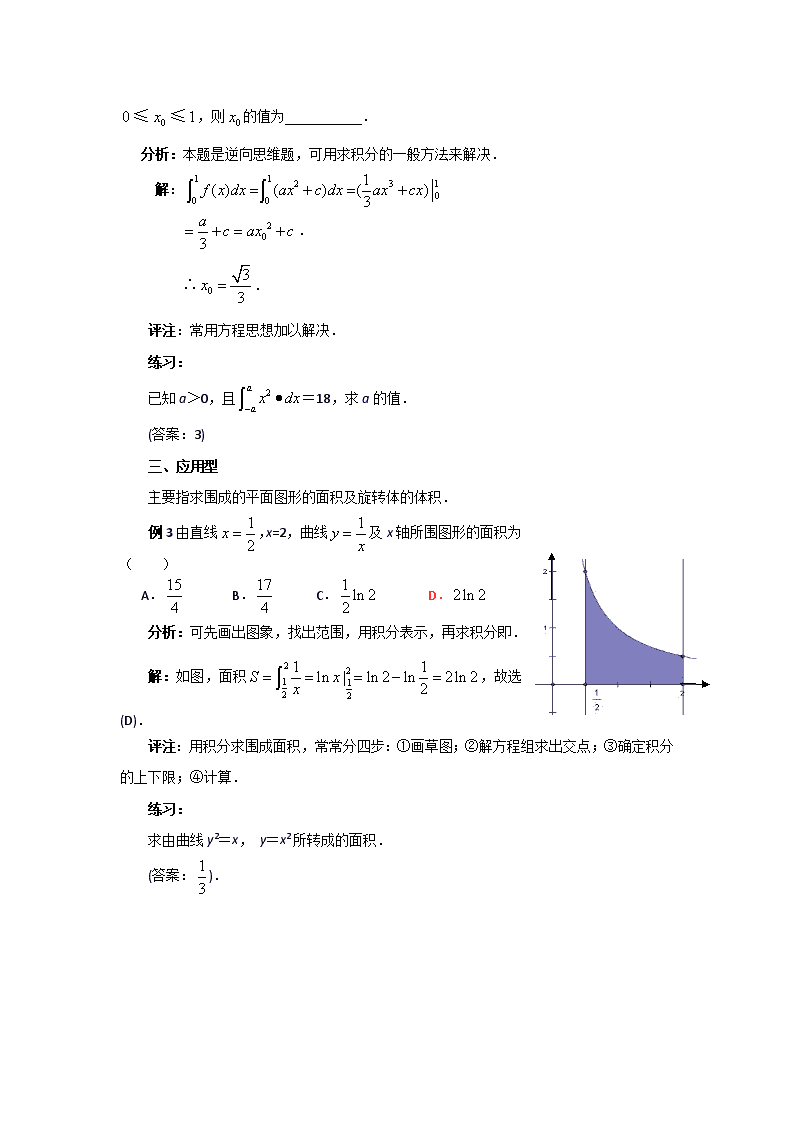
高考中的定积分定积分是微积分基本概念之一，应掌握其概念、几何意义、微积分基本定理以及简单应用．下面例析在高考中的考查方式．一、计算型是指给出定积分表达式，求其值，通常解法有：定义法，几何意义法，基本定理法及性质法等．例1计算以下定积分：⑴；⑵．分析：直接运用定义，找到一个原函数．解：⑴函数y＝的一个原函数是y＝．所以＝＝＝．⑵函数y＝sinx－sin2x的一个原函数为y＝－cosx＋cos2x．所以＝(－cosx＋cos2x)＝(－－)－(－1＋)＝－．评注：利用微积分基本定理求定积分，其关键是求出被积函数的原函数．对于被积函数是绝对值或分段函数时，应充分利用性质，根据定义域，将积分区间分成若干部分，分别求出积分值，再相加．练习：计算以下定积分：⑴；⑵．(答案：⑴；⑵)．二、逆向型主要已知定积分的值，求定积分中参数．例2设函数，若，\n，则的值为．分析：本题是逆向思维题，可用求积分的一般方法来解决．解：．．评注：常用方程思想加以解决．练习：已知a＞0，且＝18，求a的值．(答案：3)三、应用型主要指求围成的平面图形的面积及旋转体的体积．例3由直线，x=2，曲线及x轴所围图形的面积为（）A．B．C．D．分析：可先画出图象，找出范围，用积分表示，再求积分即．解：如图，面积，故选(D)．评注：用积分求围成面积，常常分四步：①画草图；②解方程组求出交点；③确定积分的上下限；④计算．练习：求由曲线y2＝x，y＝x2所转成的面积．(答案：)．