【高考调研】高考数学精品复习 课时作业(五十九) 5页

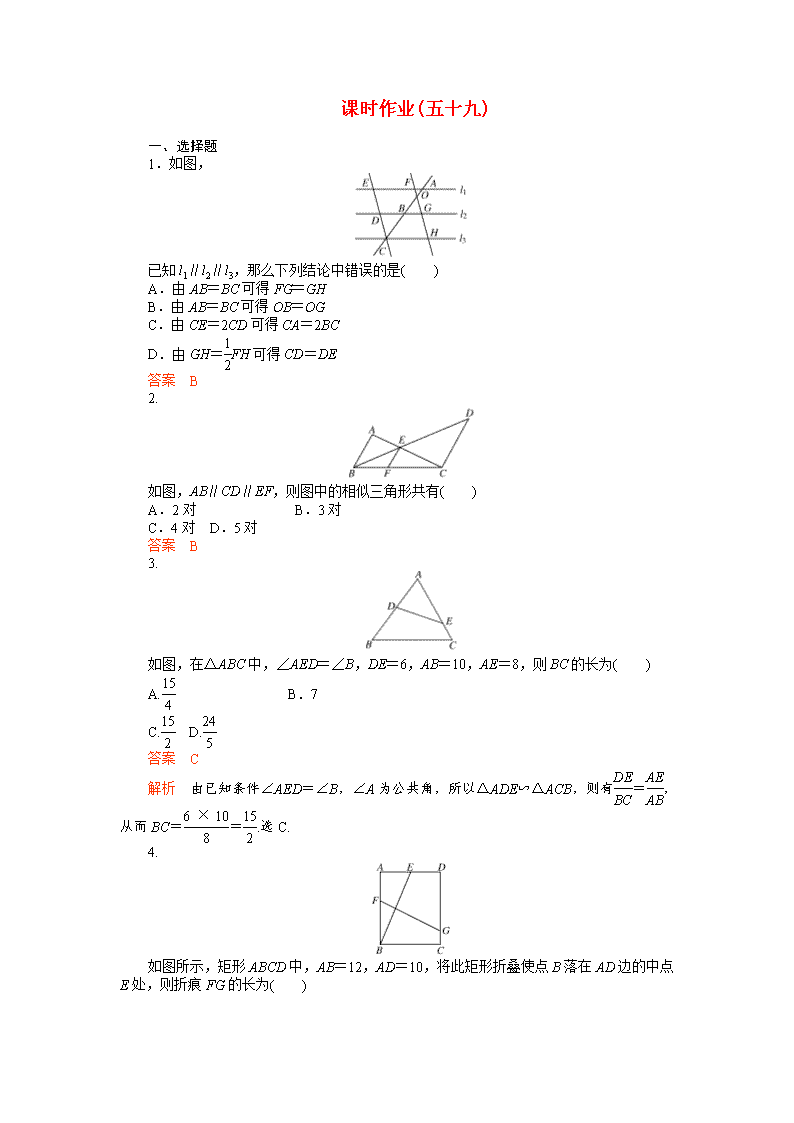
课时作业(五十九)一、选择题1．如图，已知l1∥l2∥l3，那么下列结论中错误的是(　　)A．由AB＝BC可得FG＝GHB．由AB＝BC可得OB＝OGC．由CE＝2CD可得CA＝2BCD．由GH＝FH可得CD＝DE答案　B2.如图，AB∥CD∥EF，则图中的相似三角形共有(　　)A．2对　　　　　　　B．3对C．4对D．5对答案　B3.如图，在△ABC中，∠AED＝∠B，DE＝6，AB＝10，AE＝8，则BC的长为(　　)A.　　　　　　　　B．7C.D.答案　C解析　由已知条件∠AED＝∠B，∠A为公共角，所以△ADE∽△ACB，则有＝，从而BC＝＝.选C.4.如图所示，矩形ABCD中，AB＝12，AD＝10，将此矩形折叠使点B落在AD边的中点E处，则折痕FG的长为(　　)\nA．13B.C.D.答案　C二、填空题5．在Rt△ACB中，∠C＝90°，CD⊥AB于D，若BD∶AD＝1∶4，则tan∠BCD的值为________．答案　6.如图所示，在▱ABCD中，BC＝24，E、F为BD的三等分点，则BM＝________；DN＝________.答案　12　67．两个相似三角形的面积分别为9cm2和25cm2，它们的周长相差6cm，则较大的三角形的周长为________cm.答案　158．在△ABC中，点D在线段BC上，∠BAC＝∠ADC，AC＝8，BC＝16，那么BD＝________.答案　129.如图，在△ABC中，D是AC的中点，E是BD的中点，AE交BC于F，则＝________.答案　解析　过点E作BC的平行线交AC于点M，如右图，可知M为DC的中点，故＝，＝，∴＝，＝.10.\n如图，在△ABC和△DBE中，＝＝＝.若△ABC与△DBE的周长之差为10cm，则△ABC的周长为________；若△ABC与△DBE的面积之和为170cm2，则△DBE的面积为______．答案　25cm　45cm2三、解答题11.如图所示，已知直线FD和△ABC的BC边交于D，与AC边交于E，与BA的延长线交于F，且BD＝DC，求证：AE·FB＝EC·FA.证明　过A作AG∥BC，交DF于G点．∴＝.又∵BD＝DC，∴＝.∵AG∥BC，∴＝，∴＝，即AE·FB＝EC·FA.12.如图，正方形ABCD中，AB＝2，P是BC边上与B、C不重合的任意一点，DQ⊥AP于Q.(1)试证明△DQA∽△ABP；(2)当点P在BC上变动时，线段DQ也随之变化，设PA＝x，DQ＝y，求y与x之间的函数关系式．解析　(1)∵DQ⊥AP，∴∠DQA＝90°，∠DAQ＋∠ADQ＝90°，又∵∠DAQ＋∠BAP＝90°，∴∠BAP＝∠QDA.∴△DQA∽△ABP.(2)y＝13.如图在▱ABCD中，AM⊥BC，AN⊥CD，M、N分别为垂足．求证：△AMN∽△BAC.证明　∵▱ABCD中∠B＝∠D，AD＝BC，AB∥CD又∠AMB＝∠AND＝90°\n∴Rt△AMB∽Rt△AND，∴＝＝∵AB∥CD，AN⊥CD∴AN⊥AB，∠BAM＋∠MAN＝∠BAM＋∠B＝90°∴∠B＝∠MAN∴△AMN∽△BAC(两边对应成比例且夹角相等，两三角形相似)．14.如图，在△ABC中，D、F分别在AC、BC上，且AB⊥AC，AF⊥BC，BD＝DC＝FC＝1，求AC.解析　在△ABC中，设AC为x，∵AB⊥AC，AF⊥BC，又FC＝1，根据射影定理，得AC2＝FC·BC，即BC＝x2.再由射影定理，得AF2＝BF·FC＝(BC－FC)·FC，即AF2＝x2－1.∴AF＝.在△BCD中，过D作DE⊥BC于E，∵BD＝DC＝1，∴BE＝EC＝x2.又∵AF⊥BC，∴DE∥AF.∴＝，∴DE＝＝.在Rt△DEC中，∵DE2＋EC2＝DC2，即()2＋(x2)2＝12，∴＋＝1.整理得x6＝4，∴x＝.∴AC＝.15.如图，四边形ABCD是平行四边形，点E在BA的延长线上，CE交AD于点F，∠ECA＝∠D.求证：AC·BE＝CE·AD.分析　由已知条件知CD∥BE，AD∥BC，从而△CDF∽△EAF∽△EBC.待证结论AC·BE＝CE·AD.即＝，而＝，＝，于是只要证△AFC∽△ACD，这由条件∠ECA＝∠D立即可得．证明　∵四边形ABCD是平行四边形，∴AF∥BC，∴＝.又∵AE∥CD，∴△AFE∽△DFC.∴＝，即＝＝.又∵∠ECA＝∠D，∠CAF＝∠DAC，\n∴△AFC∽△ACD，∴＝.∴＝，∴AC·BE＝CE·AD.16．已知：在△ABC中，点D在BC边上，过点C任作一直线与边AB与AD分别交于点F、E.(1)如图(1)，DG∥CF交AB于点G，当D是BC的中点时，求证：＝；(2)如图(2)，当＝时，求证：＝.证明　(1)∵DG∥CF，BD＝DC，∴BG＝FG＝BF.∵FE∥DG，∴＝.∴＝＝.(2)过点D作DG∥CF交AB于G点，∴＝.又＝，∴DC＝2BD＝BC.∵DG∥FC，∴＝＝，∴FG＝BF，∴＝＝.