数学高考总结 12页

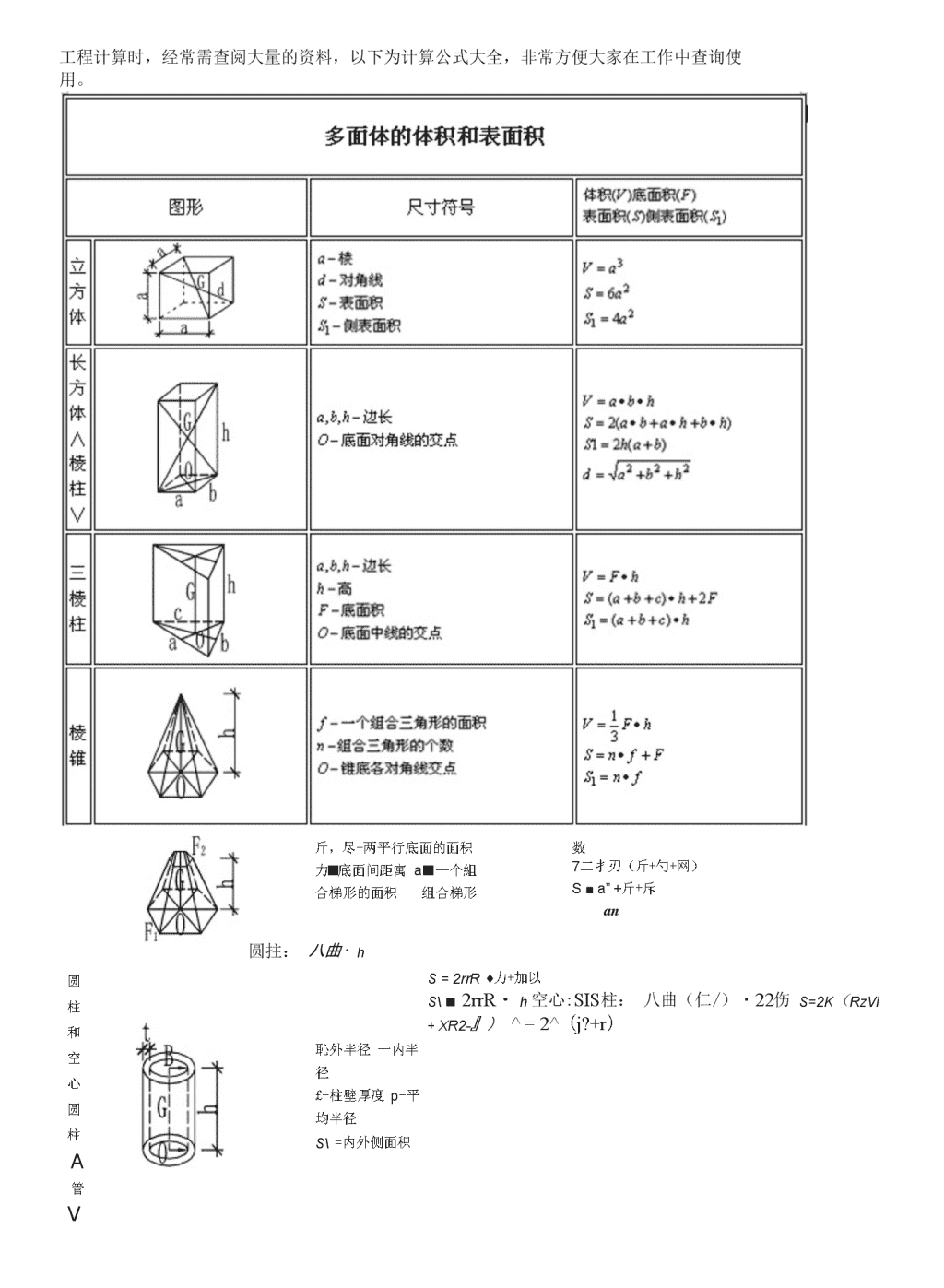
工程计算时，经常需查阅大量的资料，以下为计算公式大全，非常方便大家在工作中查询使用。斤，尽-两平行底面的面积力■底面间距寓a■—个組合梯形的面积—组合梯形数7二扌刃（斤+勺+网）S■a”+斤+斥an圆柱和空心圆柱A管V恥外半径一内半径£-柱壁厚度p-平均半径S\=内外侧面积圆拄：八曲•hS=2rrR♦力+加以S\■2rrR・h空心:SIS柱：八曲（仁/）・22伤S=2K（RzVi+XR2-』）^=2^（j?+r）\n探讨：(1)函数y=f(x)关于x=a对称f(a-^-x)=f(a-x)f(a+x)=f(a-x)也可以写成/(x)=f(2a-x)或f(-x)=f(2a+x)简证：设点(兀)在歹=/(兀)上，通itf(x)=f(2a-x)可知,y{=f(xj=f(2a-xj,即点(2d-x1,x)也在)，=/(x)上，而点(Xj,X)与点(2d-兀［,%)关于x=a对称。得证。若写成：弘+»/(一)，函数口⑴关于直线上么罟对称(2)函数y=f{x)关于点(d,b)对称of(a+x)+f(a-x)=2b上述关系也可以写W(2^+x)+f(-x)=2h或f(2a-x)+f(x)=2b简证：设点(歼，儿)在y=f(x)±,即久=心)，通f(2a-x)+f(x)=2b可知,/(2tz-%,)+/(^)=2b,所以f(2a-xl)=2b-f(xl)=2b-y\,所以点(2a-x{,2b-y\)也在y=/(兀)上,而点(2a_xi，2b_x)与(兀］,yj关于(a,b)对称。得证。若写成：f(a^x)+f(b-x)=cf函数y=/(x)关于点(筈。匸)対称(3)函数y=/(%)关于点y=b对称:假设函数关于y=b对称，即关于任一个兀值，都有两个y值与其对应，显然这不符合函数的定义，故函数自身不可能关于y=b对•称。但在曲线c(x,y)二0,则有可能会出现关于y=b对称，比如圆c(x,y)=x2+y2-4=0它会关于y二0对称。1、周期性：(1)函数y=/(x)满足如下关系系,则/⑴的周期为2TA、/(X+7)=-/(%)或如门=一1/(X)C、/(%+-)=l+/(A)nR/(X+-)=(等式右边加负号亦成立)21-/(%)2l+/(x)D、其他情形(2)函数y=/(x)满足f(a+x)=f(a-x)且f(b+x)=f(b-x),则可推出f(x)=f(2a-x)=f[b+(2a-x-b)]=f[b一(2a-x-b)]=f[x+2(b-a)]即可以得到_y=/(x)的周期为2(b-a),即可以得到“如果函数在定义域内关于垂直于x轴两条直线对称,则函数一定是周期函数”(3)如果奇函数满足/(X4-?)=-/(%)则可以推出其周期是2T,且可以推出对称轴为x=-+2kT(fcez),根据/(x)=/(x+2T)可以找出其对■称中心为伙7；0)伙wz)(以上2T工0)如果偶函数满足f(x+T)=-f(x)则亦可以推出周期是2T,且可以推出对称中心为(+2£7\0)仗wz),根据f(x)=f(x+2T)可以推出对称轴为x=T+2kT(kez)(以上\n"0)(4)如果奇函数y=fM满足f(T+x)=f(T-x)(ThO),则函数y=fM是以4T为周期的周期性函数。如果偶函数"于⑴满足/(r+x)=/(r-x)(厂工())，则函数y=f(x)是以2T为周期的周期性函数。球扇形A球楔V0Y一球半径d-弓形底凰直径力■弓形高0=?疗2方=209仙2方3$上（砒＜0・5（如/）2球缺0Yh-球缺的高一球皱半径d-平切8)3［径S曲二曲面面积£-瞬表面积?*2（一》务=2曲力=疔（%+力2）d2=4h（2r-h）圆环体A胎V圆球体平均半径Q■圆环体平均半径d-圆环体戯面言径尸-圆环体截面半径^=2xrr^T2-i/r2£W24$=4nr=f^Dd=39.478金\n虑一球半径■底面半径h-腰高\-球心腥带底圆心的距离D-中间断面直径d-底豆径桶高(S0■竺⑶?f+3分+力2)$■2鈕S=2f?Rh+/r(彳+『［)对于抛物线形桶体犷显（2"+反+3护）154对于圆形桶体7=善（2，+/）磁&■半轴r-®tt半径屮-翻i长第1课时集合的概念及运算【考点导读】1.了解集合的含义，体会元索与集合的属于关系；能选择自然语言，图形语言，集合语言描述不同的具体问题，感受集合语言的意义和作用.2.理解集合之间包含与相等的含义，能识别给定集合的子集；了解全集与空集的含义.3.理解两个集合的交集与并集的含义，会求两个集合的交集与并集；理解在给定集合中一个子集补集的含义，会求给定子集的补集；能使用文氏图表达集合的关系及运算，体会直观图示对理解抽象概念的作用.4.集合问题香与函数，方程，不等式有关，其中字母系数的函数，方程，不等式要复杂一些，综合性较强，往往渗透数形思想和分类讨论思想.\n常用图形求面积公式图形尺寸符号面积(F)表面积(S)正方形0a4-边长0-对角线c2-7f-0.7?dd=1.414?=1.414、/?5.已知下列命题:①定义在/?上的函数.f⑴满足.f(2)>/(I),则函数.f(x)是/?上的增函数;②定义在尺上的函数/(兀)满足/(2)>/(I),则函数/(兀)在R上不是减两数；③定义在R上的函数/(兀)在区间(-00,0］上是增函数，在区间［0,+oo)上也是增函数，则函数/(兀)在/?上是增函数；④定义在R上的函数/(兀)在区间(-00,0］上是增函数，在区间(0,+00)上也是增函数，则函数/(兀)在上是增函数.其中正确命题的序号有@.【范例解析】3例.求证：(1)函数f(x)=-2x2+3x-l在区间(-co,-］_上是单调递增函数；42x-l(2)函数f(x)=在区间(-00,-1)和(―l，+oo)上都是单调递增函数.X+1分析：利用单调性的定义证明函数的单调性，注意符号的确定.3证明：(1)对于区间(-00,—］内的任意两个值X］,X2,且X!0故zIVn<0-即/3)一/也)<0,即fgjg.(西+1)(兀2+I)2x-l所以，函数/(%)=——在区间(-O-1)上是单调增函数.x+12r-l同理，对于区间(-1，+00)，函数/(%)=-一是单调增函数；兀+12%——]所以，函数/(%)=-一在区间(-00,-1)和(-1,+00)上都是单调增函数.X+1点评：利用单调性定义证明函数的单调性，一般分三步骤：(1)在给定区间内任意取两值召，兀2；(2)作差/(西)-/(%2)，化成因式的乘积并判断符号；(3)给出结论.例2.确定函数/(X)=.-的单调性.a/1—2x分析：作差后，符号的确定是关键.解：由1一2兀>0,得定义域为(-oo,l).对于区间(-co,丄)内的任意两个值西，x2,且x,0,.••/(^)-/(%2)<0,即/(州)0,(x2+2)>0得,(%!+2)(x2+2)〉0,:A-2a<0第4课函数的奇偶性【考点导读】1.了解函数奇偶性的含义，能利用定义判断一些简单函数的奇偶性；2.定义域对奇偶性的影响：定义域关于原点对称是两数为奇函数或偶函数的必要但不充分条件；不具备上述对称性的，既不是奇函数，也不是偶函数.【基础练习】\nY4_11•给出4个函数:①f(x)=x5+5x；②f(x)=—；③/(%)=-2%+5；④f(x)=ex-e^x.其中奇函数的冇①④：偶函数的冇②；既不是奇函数也不是偶函数的冇③.2.设函数/(兀)=Z)U为奇函数，则实数a=—1.3.下列两数屮，在其定义域内既是奇函数乂是减函数的是(A)q■1yA-y=一尢,xeRB.y=sinx,xeRC.y=x,xeRD・y=(—),xeR\n【范例解析】例1.判断下列函数的奇偶性:(1)/(X)(1+2”尸2X(2)f(x)=lg(x+Vx2+1)；91(3)/(x)=lgx24-lg—;(5)f(x)=4-x—1|+1；⑷y(x)=(i-x)fM=-x2+x(x>0),x2+x(X<0).分析：判断函数的奇偶性，先看定义域是否关于原点对称，再利用定义判断.解：(1)定义域为xwR,关于原点对称;2加.(1+27)222t・2~x(l+2r)2~T-所以/(x)为偶函数.(2)定义域为x丘R,关于原点对称；*/f(—x)+f(x)=lg(—x+\lx2+1)+lg(x+yjx2+1)=lg1=0,/(-x)=-/(x),故.f(x)为奇函数.(3)定义域为兀w(—8,02(0,+8),关于原点对称；v/(x)=0,A/(-x)=-/(%)且/(—兀)=/(兀),所以于(力既为奇函数乂为偶函数.(4)定义域为xe|-l,l),不关于原点对称；故/(兀)既不是奇函数也不是偶函数.(5)定义域为xeRf关于原点对称；・・・/(一1)=4,/(1)=2,则/(一1)工/(1)且/(-1)^-/(1),故/(兀)既不是奇函数也不是偶函数.(6)定义域为xwR,关于原点对称;-(-X)2+(-X)(-X>0),(-X)2+(-X)(-X<0).-x2-x(x>0),x2-x(X<0).又/(0)=0,-x-x(x<0),"Hego)")T⑴,故加为奇函数•点评：判断函数的奇偶性，应首先注意其定义域是否关于原点对称；其次，利用定义即/(-x)=-/U)或/(-X)=/(兀)判断，注意定义的等价形式/(-x)+/(x)=0或/(-x)-/(x)=0.例2.已知定义在/?上的函数/(Q是奇函数，且当兀〉0时，/(x)=x2-2x+2,求函数/(x)的解析式，并指出它的单调区间.分析：奇函数若在原点有定义，则/(0)=()・解：设x<0,则一x>0,/(-x)=x2+2x+2.\n又/(力是奇函数,/./(-X)=-/(%),.\/(x)=-/(-x)=-x2-2x-2.当x=0时，/(0)=0.x2-2x+2,x>0综上，/(x)的解析式为f(x)=0,x=0.—x~—2x—2,兀v0作出.f(x)的图像,可得增区间为(-00,-1］,［1,+Q,减区间为［-1,0),(0,1］.点评：(1)求解析式时x=0的情况不能漏；(2)两个单调区间之间一般不用“U”连接；(3)利用奇偶性求解析式一般是通过“-兀”实现转化:(4)根据图像写单调区间.【反馈演练】1.已知定义域为R的函数/*(兀)在区间(&+oo)上为减函数，且函数y=/(x+8)为偶函数，则(D)A•/⑹〉/⑺B./⑹〉九9)C./(7)>/⑼D./(7)>/(10)2.在R上定义的函数/(兀)是偶函数，且/(x)=/(2-x),若/(兀)在区间［1,2］是减函数，则函数/、(兀)(B)A.在区间［-2,-1］上是增函数，区间［3,4］上是增函数B.在区间［-2,-1］上是增函数，区间［3,4］上是减函数C.在区间［-2,-1］上是减函数，区间［3,4］上是增函数D.在区间［-2,-1］上是减函数，区间［3,4］上是减函数3.设1,1,*3},则使函数y=的泄义域为R且为奇函数的所有Q的值为1,3・51—4.设函数/(x)(xE/?)为奇函数，/(l)=-,/(x+2)=/(x)+/(2),则〃5)=2•5.若函数/⑴是定义在R上的偶函数，在(—oo,0］上是减函数,且/⑵=0,则使得/(%)<0的兀的取值范由是_（一2,2）.1.已知函数于（兀）=竺土Z）是奇函数.又f（1）=2,/（2）＜3,求a,方，c的值;bx+c解：山/(-x)=-/(x),-hx+c=-(hx+c),得c=0・乂/(1)=2,得d+l=2/?，而/(2)＜3,得纟也＜3,解得一1＜。＜2.又«eZ,:.a=0或1.Q+1\n若d=0，贝iJ/?=-0Z,应舍去；若a=\，则h=\eZ.2所以，a=l,b=l,c=0・土方量计算的基本方法土方量计算的基本方法主要有平均高度法和平均断血法两种。1.平均高度法土方量计算公式表（四方棱柱体法）方格类别计算图形计算公式全挖（或全填）匕1ja匚V=a2/4X(h]+112+113+I")半挖hlh4Bh253V=(V+c)/2XaX(Eh/4)=a/8X(b+c)X(In+In)三挖hlch4@bh2ah3三个角挖(或填)：V=(a2-bc/2)XEh/5=1/5X(a2-bc/2)X(hi+h2+113)一个角填(或挖)：V=(bc/2)XEh/3=l/6XbXcXI14注：1.表中a为方格边长，b、c为计算图形相应的两个边长；2.hl、h2、h3、h4分为各角点的施工高度;3.工h为各计算图形相应的挖方或填方的施工高度总和，用绝对值代入;4.V为挖方或填方的体积（m3）0当采用平均断而法计算基槽、管沟或路基土方量时，可先测绘出纵断而图，再根据沟槽基底的宽、纵向坡度及放坡宽度，绘出在纵断面图上各转折点处的横断面，算出各横断面面积后便可\n用平均断面法计算各段的土方量,BIJ：V二(F1+F2)XL1/2+(F2+F3)XL2/2+(F3+F4)XL3/2+注:Fl、F2……表示横断面面积;LI、L2表示断面Z间距离。