高考数学专题04高考考前调研卷四 15页

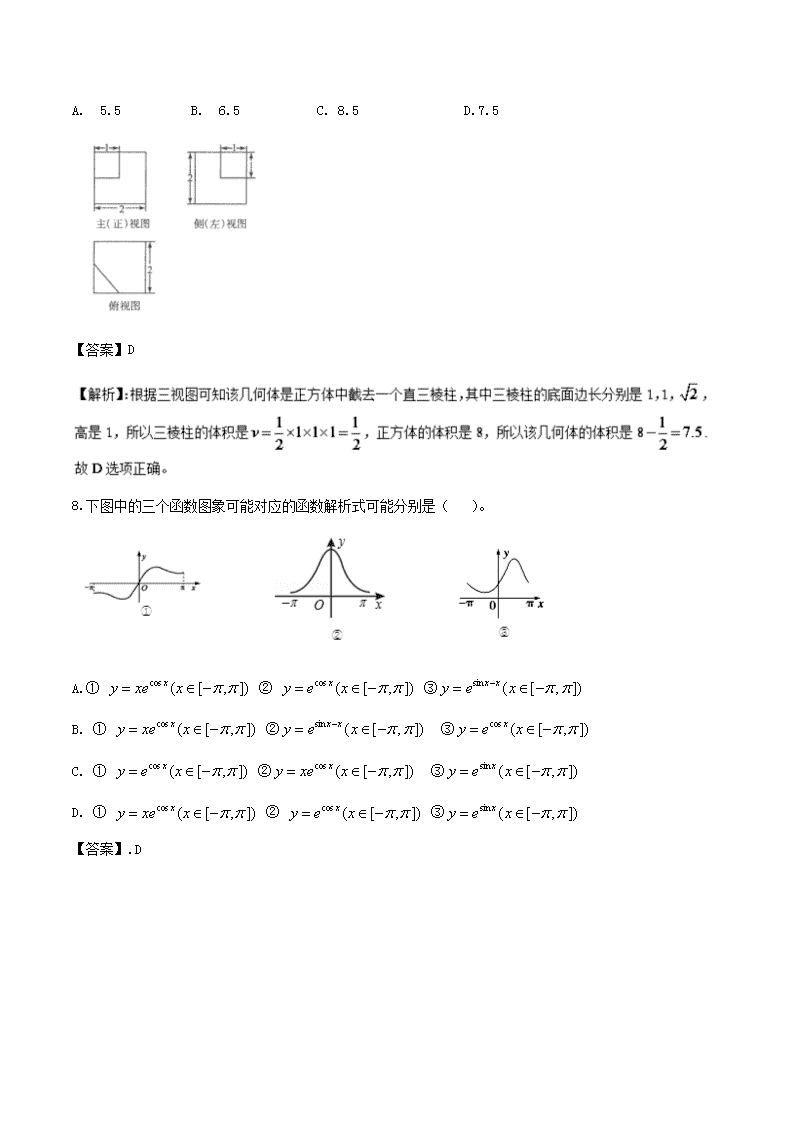
专题04高考考前调研卷（四）【命题说明】命题者是在认真研究近几年新课标全国卷高考试题，命题时严格按照全国Ⅰ卷格式编排，以最新发布的2018年全国卷《考试说明》为依据，内容确保不超纲。调研卷体现高考“前瞻性”和“预测性”。试卷力争做到形、神与新课标全国卷风格一致，让学生和教师有“高考卷”的感觉。试卷中知识点分布、试卷的总字数（包括各科选择题的题干字数、大题材料的长度、信息的有效性）、选项文字的长度、答案的规范、难易度的梯度等，都要符合高考试卷特点。一．选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合，，则（）A．B．C．D．【答案】C【解析】：由解得：，所以，所以。故选项C正确。2.已知向量若，则（　　）A．﹣1B．1C．D．【答案】C【解析】：因为，所以，所以，故选项C正确。3.复数满足，则（）A．B．C．D．【答案】B【解析】根据已知得：，所以，所以，故选项B正确。4.“春晚歌舞是抢红包背景乐”成了春晚被转发频次最高的“段子”之一。抢红包涉及平台有支付宝、微信、QQ、微博四个；如果夫妻两人参与其中一个抢红包活动，每人参与等可能的，则夫妻二人参与同一个平台的概率是（）。A.B.C.D.【答案】B\n【解析】所有可能情况有：，夫妻二人参加同一个活动的情况有四种，所以所求概率是，故选项B正确。5.已知抛物线与双曲线有一个公共的焦点，两曲线在第一象限的交点连线经过公共焦点，（如图），则双曲线的渐近线方程是（）。A．B．C．D．【答案】D6.函数叫做“取整函数”，其中符合[x]表示x的整数部分，及[x]是不超过x的最大整数，例如[2]=2;[2.1]=2;[-2.2]=-3,那么[lg1]+[lg2]+[lg3]+…………+[lg2016]=（）A.2016B.2015C.4941D4940【答案】C【解析】：[lg1]+[lg2]+[lg3]+…………+[lg2016]=[lg1]+……+[lg9]+[lg10]+……+[lg99]+[lg100]+…………+[lg999]+[lg1000]+……+[lg2016]=0+1.故选项C正确。7.如图是某几何体的三视图，则该几何体的体积是（）。\nA.5.5B.6.5C.8.5D.7.5【答案】D8.下图中的三个函数图象可能对应的函数解析式可能分别是（）。A.①②③B.①②③C.①②③D.①②③【答案】.D\n9.已知实数满足约束条件，则的最大值是（　　）A．2B．32C．6D．64【答案】D【解析】：画出满足条件的平面区域，如图示：由，解得：A（﹣2，2），由设z=y﹣2x得；y=2x+z，由图象得直线y=2x+z过A（﹣2，2）时取到最大值，z的最大值是：6，所以，所以的最大值是故选项D正确。10.正项等比数列中的，是函数的极值点，则（）。A．　　　　B．　　　C．　　　　　　D．【答案】D【解析】的导函数是，因为正项等比数列中的，\n函数的极值点，所以=7，再根据等比数列的性质知：，所以，所以。所以D选项正确。11.直三棱柱ABC-各顶点都在同一个球面上，若,正三棱柱的高是2，若记球O的体积为V，球O的表面积是S，则（）。A.B.C.D.【答案】B12.已知函数，若方程有四个不同实数根，则的取值范围是（）。A.B.C.D.不确定【答案】A【解析】：不妨设，根据二次函数的对称性知且，，由，知且，（其中）∴]，故的取值范围是。故A选项正确。二．填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）\n13.执行如图的程序，若输入x=2016，则输出i=___________。【答案】714.已知，且则【答案】；【解析】:因为，则，因此，所以，于是．15.设定义在R上的奇函数，满足对任意的都有，且时，，则\n【答案】-1；16.设是等比数列{}的前项和，＞0，若则的最小值为　　．【答案】24【解析】：因为＞0，前n项和>0，数列是等比数列，所以根据等比数列的性质得：、、构成等比数列，所以，所以，因为所以当且仅当及=6时等号成立。所以最小值是24.三．解答题（解答应写出文字说明，证明过程或演算步骤）17.（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，且．（1）求角A的值；（Ⅱ）当取得最大值时，试判断△ABC的形状．【解析】：（1）由结合正弦定理得:…………2分化简得：，移项得：即：，…………4分所以，\n所以………………6分18.（本小题满分12分）三棱锥D-ABC中，且平面DAC平面ACB，且ADDC,ACBC,AD=DC=1,AB=2.(1)求值AD平面BCD；（2）在CD上找一点F，使AD∥平面EFB，并且求出F-BCE的体积。【解析】（1）证明：因为平面DAC平面ACB，设E是AC中点，连接DE，因为△DAC是等腰三角形，所以DEAC,…………3分又因为ACBC,所以BC平面DAC，所以BCAD，又因为ADDC，且直线DC与BC相交，所以AD平面BCD；…………6分\n19.（本小题满分12分）微信是腾讯公司推出的一个为智能终端提供即时通讯服务的免费应用程序，某微商为了调查客户每天微信用户使用微信的时间，使用微信的时间分成5组：（0，2]，（2，4]，（4，6]，（6，8]，（8，10]分别加以统计，得到如图所示的频率分布直方图．\n（Ⅰ）分别求第三，四，五组的频率；（II）根据频率直方图估计该调查使用微信的平均时间；（III）从第3，4，5组中随机抽取10名微商客户做初次调查．问每组抽取多少人？若从10名客户中再次随机抽取2名客户进行再次调查，问这2名客户不在同一组的概率？【解析】（Ⅰ）解：第三组的频率是0.150×2=0.3，第四组的频率是0.100×2=0.2，第五组的频率是0.050×2=0.1．…（4分）（II）平均使用微信的时间为：0.0252×1+0.1752×3+0.152×5+0.12×7+0.052×9=4.9（小时）（7分）20.（本小题满分12分）已知离心率为的椭圆C：（a＞b＞0）经过点（1，）．（I）过右焦点F的直线与椭圆C交于不同的两点M，N，是否存在直线，使得△BFM与△BFN的面积比值为2？若存在，求出直线的方程；若不存在，说明理由．（Ⅱ）若直线：y=kx+m与椭圆C相切于P点，且与直线x=﹣4相交于Q点，求证：直线PF1垂直于直线QF1．（其中F1是左焦点）【解析】（1）由于椭圆C：（a＞b＞0）的离心率为，则a=2c，b=c，又由椭圆C经过点（1，），则c2=1，故a=2，b=，\n所以椭圆方程为．…………3分△BFM与△BFN的面积比值为2等价于FM与FN比值为2当直线斜率不存在时，FM与FN比值为1，不符合题意，舍去；当直线斜率存在时，设直线的方程为y=k（x﹣1），直线的方程代入椭圆方程，消x并整理得（3+4k2）y2+6ky﹣9k2=0设M（x1，y1），N（x2，y2），则y1+y2=﹣①，y1y2=﹣②由FM与FN比值为2得y1=﹣2y2③由①②③解得k=±，因此存在直线：y=±（x﹣1）…………6分∴P点的坐标为．…………8分由解得y=﹣4k+m．∴Q点的坐标为（﹣4，﹣4k+m）．…………9分\n由F1（﹣1，0），求得，，∴．………………11分∴直线PF1垂直于直线QF1．…………12分21.（本小题满分12分）已知。（I）求函数在上的最小值；（II）若，恒成立，求正整数k的值．（II）∵，∴x﹣1＞0．\n则问题转化为恒成立且，…………8分设函数，则，再设，则．∵），∴m′（x）＞0，则m（x）=x﹣lnx﹣2在（1，+∞）上为增函数，∵∴，使．…………10分∴当时，，∴在（1，x0）上递减，时，，∴在上递增，∴h（x）的最小值为．∵，∴lnx0+1=x0﹣1，代入函数得，∵，且k＜h（x）对恒成立，∴k＜h（x）min=x0，∴k≤3，∴k的值为1，2，3．…………12分请考生在第22，23题中任选一题作答，如果多做，则按照所做的第一题计分，作答时请写清题号。22（本题满分10分）坐标系与参数方程在极坐标系中，已知曲线C：，（1）过极点O的直线与曲线C交于A，B两点，且AB=，求直线的方程．（2）D、F为曲线C的两点，以极点为原点，极轴为轴非负半轴的直角坐标中，曲线H：上一点P，求∠DPF的最大值。【解析】（1）曲线C：，变为，化为x2+y2=2y，配方为x2+（y﹣1）2=1，\n圆心为（0，1），半径r=1．…………2分由题意可知直线l的斜率存在，设直线l的方程为y=kx，则圆心到直线l的距离d=．∵|AB|=2，∴，化为=3．解得k=．∴直线l的方程为．…………5分23（本题满分10分）不等式选讲：已知函数。（1）当时，不等式的解集。（2）若，使得成立，求实数的取值范围．【解析】．（Ⅰ）当时，由，即得，两边平方整理得，，解得或，∴原不等式的解集为（﹣∞，﹣1]∪[，+∞）…………5分（Ⅱ）由得，令，即……………………8分\n故h（x）min=h（﹣）=﹣，故可得到所求实数a的范围为[﹣，+∞）．…………10分