【物理】2019届二轮复习求3个力的合力的6种方法学案（全国通用） 6页

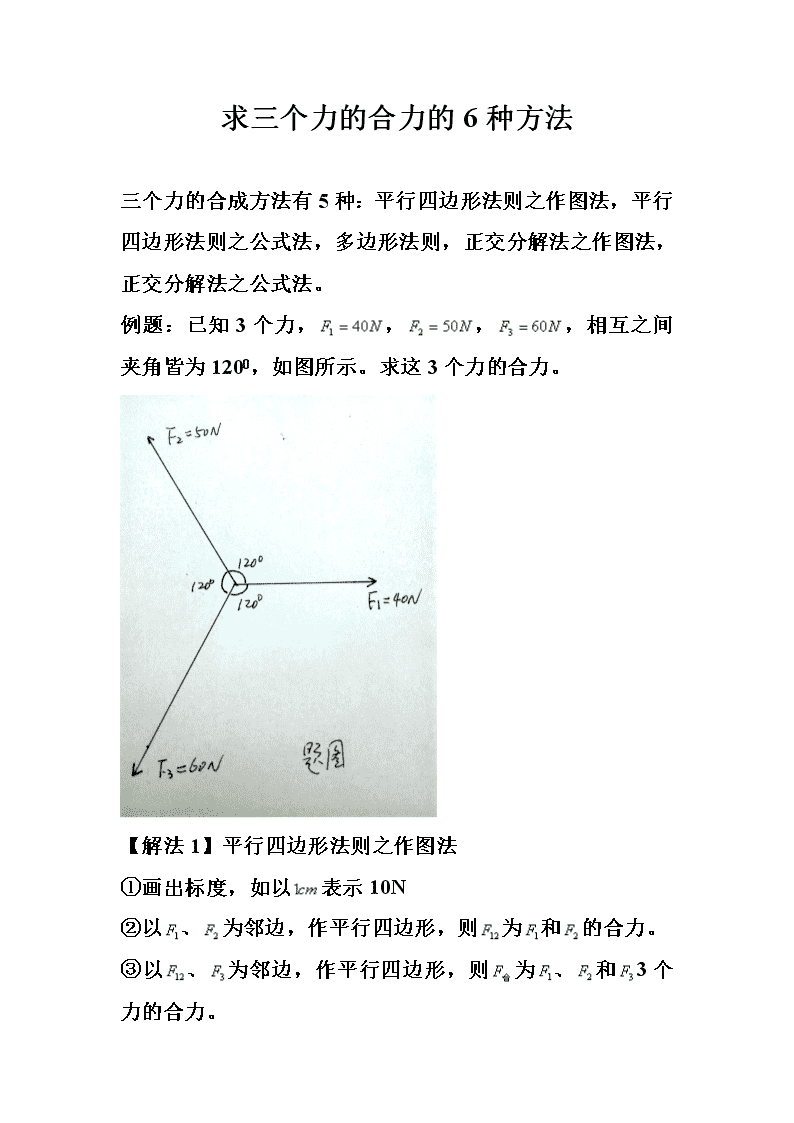
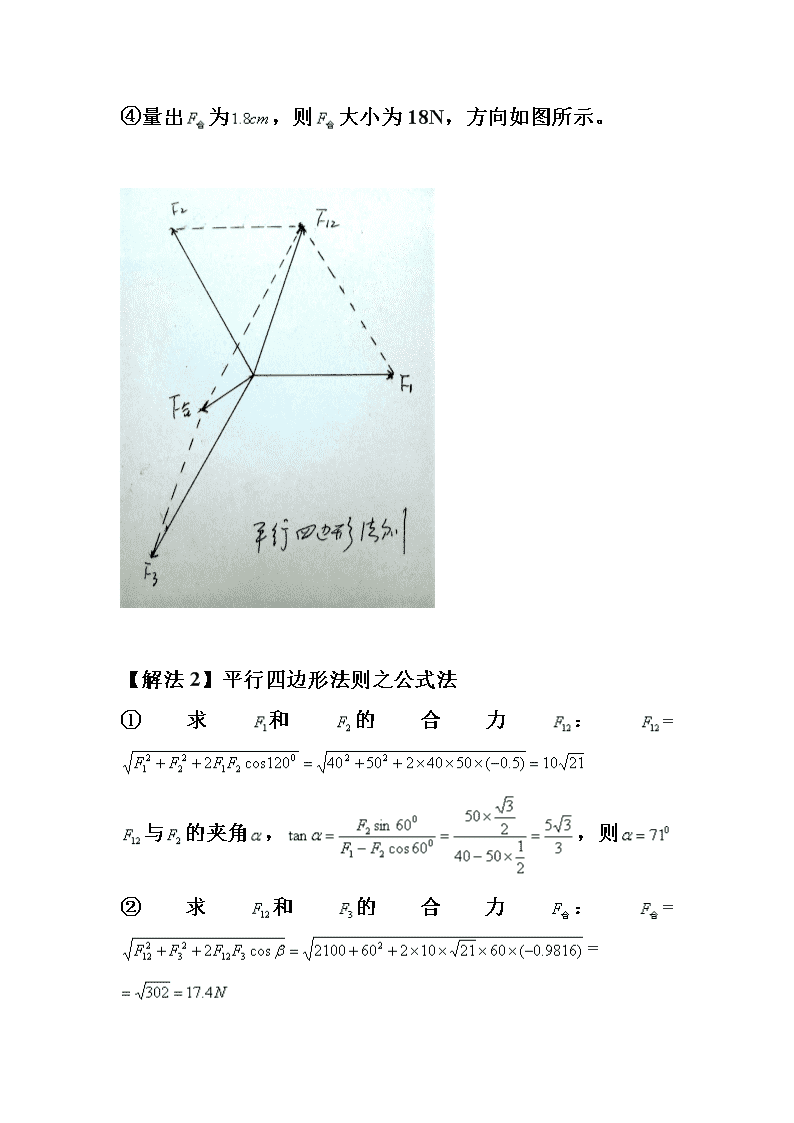
求三个力的合力的6种方法 ‎ ‎ 三个力的合成方法有5种：平行四边形法则之作图法，平行四边形法则之公式法，多边形法则，正交分解法之作图法，正交分解法之公式法。‎ 例题：已知3个力，，，，相互之间夹角皆为1200，如图所示。求这3个力的合力。‎ ‎【解法1】平行四边形法则之作图法 ①画出标度，如以表示10N ②以、为邻边，作平行四边形，则为和的合力。‎ ③以、为邻边，作平行四边形，则为、和3个力的合力。‎ ④量出为，则大小为18N，方向如图所示。‎ ‎【解法2】平行四边形法则之公式法 ①求和的合力：=‎ 与的夹角，，则 ②求和的合力：==‎ 其中，‎ ‎【解法3】多边形法则之作图法 ①画出标度，如以表示10N ②从矢量尾端作矢量，从矢量尾端作矢量 ③从矢量首端到矢量尾端作矢量，把、和3个矢量封闭成闭合多边形，则为、和3个力的合力。‎ ④量出为，则大小为18N，方向如图所示。‎ ‎【解法4】多边形法则之公式法 ①求和的合力：=（根据余弦定理）‎ 与的夹角，（根据正弦定理），则，‎ ②求和的合力：==‎ 其中，‎ ‎【解法5】正交分解法之作图法 ①画出标度，如以表示10N；‎ ②建立直角坐标系，使在轴上；‎ ③将、分解为、和、；‎ ④画出和 ⑤画出，量出为，则大小为18N，方向如图所示。从图可以看出，所谓多边形法则，实际上是三角形法则的进步。三角形法则适用于求两个力的合力，多边形法则适用于求3个及以上个力的合力。‎ ‎【解法6】正交分解法之公式法。‎ ①建立直角坐标系，使在轴上；‎ ②将、分解为=-、=和=-、=；‎ ④求出=和=‎ ⑤求出=3N.‎ 从以上可以看出，作图法比较直观，公式法比较精确。总的看来，正交分解法应用比较广泛，因为把普通三角形化成了直角三角形，计算起来比较方便。‎ ‎（写于‎2018-11-27‎）‎