河南省南阳市六校2019-2020学年高二下学期第一次联考数学（文）试题 Word版含解析 19页

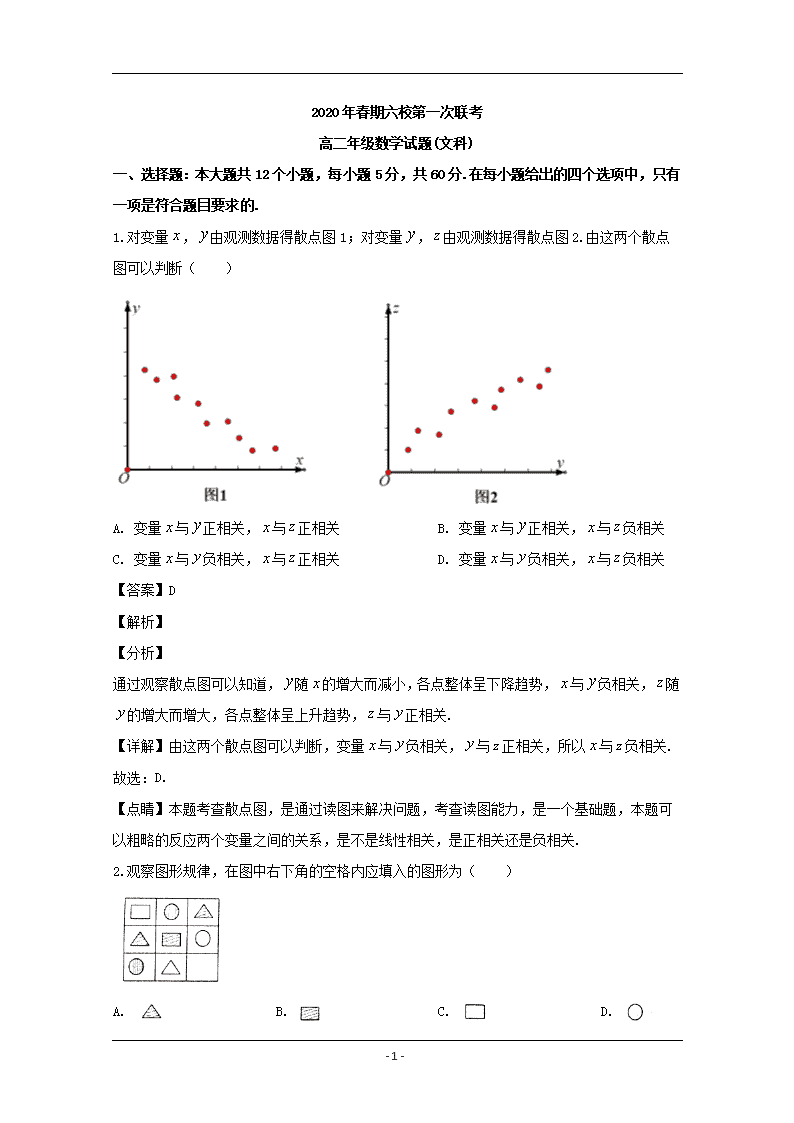
- 1 - 2020 年春期六校第一次联考 高二年级数学试题(文科) 一、选择题：本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 1.对变量 ， 由观测数据得散点图 1；对变量 ， 由观测数据得散点图 2.由这两个散点 图可以判断（ ） A. 变量 与 正相关， 与 正相关 B. 变量 与 正相关， 与 负相关 C. 变量 与 负相关， 与 正相关 D. 变量 与 负相关， 与 负相关 【答案】D 【解析】 【分析】 通过观察散点图可以知道， 随 的增大而减小，各点整体呈下降趋势， 与 负相关， 随 的增大而增大，各点整体呈上升趋势， 与 正相关. 【详解】由这两个散点图可以判断，变量 与 负相关， 与 正相关，所以 与 负相关. 故选：D. 【点睛】本题考查散点图，是通过读图来解决问题，考查读图能力，是一个基础题，本题可 以粗略的反应两个变量之间的关系，是不是线性相关，是正相关还是负相关. 2.观察图形规律，在图中右下角的空格内应填入的图形为（ ） A. B. C. D. x y y z x y x z x y x z x y x z x y x z y x x y z y z y x y y z x z - 2 - 【答案】B 【解析】 分析：观察图形不难发现每行有两个阴影图形，三个图形有长方形、圆、三角形 详解：其规律是每行有方块，三角形，圆形各一个，且有两块是有阴影部分，照此规律，第 三行第三格应填方块，由于前两格只有一格有阴影部分，故第三格应是阴影部分的方块 故选 点睛：本题属于规律题，只要观察图形做出判断不难发现规律． 3.余弦函数 偶函数， 是余弦函数，因此 是偶函数， 以上推理（ ） A. 结论不正确 B. 大前提不正确 C. 小前提不正确 D. 全不正确 【答案】C 【解析】 【分析】 分别判断大前提、小前提、结论的正确性，选出正确的答案. 【详解】大前提：余弦函数是偶函数，这是正确的； 小前提： 是余弦函数.我们把 叫余弦函数，函数 是余弦函数复合一个二次函数，故小前提不正确； 结论： 是偶函数. ,所以结论正确，故 本题选 C. 【点睛】本题考查了判断三段论推理中每段推理 正确性，解题的关键是对偶函数的正确理 解. 4.在建立两个变量 与 的回归模型中，分别选择了 4 个不同的模型，结合它们的相关指数 判断，其中拟合效果最好的为（ ） A. 模型 1 的相关指数 为 0.3 B. 模型 2 的相关指数 为 0.25 C. 模型 3 的相关指数 为 0.7 D. 模型 4 的相关指数 为 0.85 【答案】D 是 的 B 2( ) cos(2 3)f x x= − 2( ) cos(2 3)f x x= − 2( ) cos(2 3)f x x= − ( ) cosf x x= 2( ) cos(2 3)f x x= − 2( ) cos(2 3)f x x= − 2 2 2( ) cos(2 3) ( ) cos[2( ) 3] cos(2 3) ( )f x x f x x x f x= − ⇒ − = − − = − = y x 2R 2R 2R 2R 2R - 3 - 【解析】 【分析】 根据相关指数 的大小作出判断即可得到答案． 【详解】由于当相关指数 的值越大时，意味着残差平方和 越小，即模型的拟合效果越好， 所以选项 D 中的拟合效果最好． 故选 D． 【点睛】本题考查回归分析中相关指数的意义，解题的关键是熟悉相关指数与拟合度间的关 系，属于基础题． 5.已知程序框图如图所示，则输出的 ( ) A. B. C. D. 【答案】B 【解析】 【分析】 根据流程图逐步运算,直到跳出循环,即可求得答案. 【详解】 , , ; 2R  2 1 2 2 1 1 ( ) = ( ) n i i i n i i y y y R y = = − − − ∑ ∑  2 1 ( ) n i i i y y = −∑ S = 47 60 7 12 37 60 5 12 1a = 1n = 0S = - 4 - , , ; , , ; , , ; , , ; 跳出循环,输出结果 . 故选:B. 【点睛】本题考查流程图,掌握流程图基本知识是解题关键,考察了分析能力,属于基础题. 6.假设有两个变量 与 的 列联表如下表： 对于以下数据，对同一样本能说明 与 有关系的可能性最大的一组为（ ） A. ， ， ， B. ， ， ， C. ， ， ， D. ， ， ， 【答案】B 【解析】 【分析】 当 ad 与 bc 差距越大，两个变量有关的可能性就越大，检验四个选项中所给的 ad 与 bc 的差 距，只有第二个选项差距大，得到结果． 【详解】解：根据观测值求解的公式可以知道， 当 ad 与 bc 差距越大，两个变量有关的可能性就越大， 检验四个选项中所给的 ad 与 bc 的差距： 1S = 1a = − 2n = 11 2S = − 1a = 3n = 1 11 2 3S = − + 1a = − 4n = 1 1 1 71 2 3 4 12S = − + − = 1a = 5n = 7 12S = x y 2 2× 1y 2y 1x a b 2x c d x y 2a = 3b = 4c = 5d = 5a = 3b = 3c = 4d = 3a = 6b = 2c = 5d = 5a = 3b = 4c = 3d = A :ad bc 10 12 2− = − = − B:ad bc 20 9 11− = − = - 5 - 显然 中 最大. 故答案为 B. 【点睛】本题考查独立性检验，得出 ad 与 bc 差距越大，两个变量有关的可能性就越大是解 决问题的关键，属基础题． 7.用反证法证明“至少存在一个实数 ，使 成立”时，假设正确的是（ ） A. 至少存在两个实数 ，使 成立 B.至多存在一个实数 ，使 成立 C. 不存在实数 ，使 成立 D. 任意实数 ， 恒成立 【答案】C 【解析】 【分析】 根据反证法的原理可直接判断得到结果. 【详解】根据反证法的原理知：假设是对“至少存在一个实数 ”的否定， 即“不存在实数 ，使 成立”. 故选： . 【点睛】本题考查反证法原理的应用，属于基础题. 8.某工厂产品的组装工序图如图所示，箭头上的数字表示组装过程中所需的时间（单位：分 钟），则组装该产品所需要的最短时间为（ ） A. 12 分钟 B. 13 分钟 C. 15 分钟 D. 17 分钟 【答案】C 【解析】 【分析】 由已知中的工序流程图，计算出每条组装工序从开始到结束的时间，比较即可得到答案． 【详解】从 需 8 分钟， C:ad bc 15 12 3− = − = D :ad bc 15 12 3− = − = B ad bc− 0x 03 0x > 0x 03 0x > 0x 03 0x > 0x 03 0x > x 3 0x > 0x 0x 03 0x > C A B E F→ → → - 6 - 从 需 10 分钟， 以上两条工序可同时进行最少需要 10 分钟， 由 需 5 分钟，故所需的最短时间为 15 分钟. 故选 C. 【点睛】本题考查的知识点是工序流程图，关键是分析所给流程图，从中获得正确信息，属 于基础题． 9.有甲、乙、丙、丁四位大学生参加创新设计大赛，只有其中一位获奖，有人走访了这四位 大学生，甲说：“是丙获奖.”乙说：“是丙或丁获奖.”丙说：“乙、丁都未获奖.”丁说： “我获奖了.”这四位大学生的话只有两人说的是对的，则获奖的大学生是（ ） A. 甲 B. 乙 C. 丙 D. 丁 【答案】D 【解析】 【分析】 根据四位大学生 话只有两人说的是对的，假设其中一人说的对，如果和条件不符合，就说 明假设的不对，如果和条件相符，则按假设的方法解决问题. 【详解】若甲说的对，则乙、丙两人说的也对，这与只有两人说的对不符，故甲说的不对； 若甲说的不对，乙说的对，则丁说的也对，丙说的不对，符合条件，故获奖的是丁； 若若甲说的不对，乙说的不对，则丁说的也不对，故本题选 D. 【点睛】本题考查了推理的应用，假设法是经常用的方法. 10.观察下列各式： ， ， ，…，则 的末两位数字为（ ） A. 49 B. 43 C. 07 D. 01 【答案】C 【解析】 【分析】 先观察前 5 个式子的末两位数的特点，寻找规律，结合周期性进行判断即可. 【 详 解 】 观 察 ， ， ， ， ，…，可知末两位每 4 个式子一个循环， 到 一共有 1008 个式子，且 ，则 的末两位数字与 的末两位数字相同，为 07. 的 A C D F→ → → F G→ 27 49= 37 343= 47 2401= 10097 27 49= 37 343= 47 2401= 57 2401 7 16807= × = 67 16807 7 117649= × = 27 49= 10097 1008 4 252÷ = 10097 57 - 7 - 故选：C. 【点睛】本题主要考查归纳推理的应用，根据条件寻找周期性是解决本题的关键. 11.在平面中，与正方形 的每条边所成角都相等的直线与 所成角的余弦值为 . 将此结论类比到空间中，得到的结论为:在空间中，与正方体 的每条棱所 成角都相等的直线与 所成角的余弦值为（ ） A. B. C. D. 【答案】B 【解析】 【分析】 首先根据题中条件可知该直线是正方体的体对角线，然后根据余弦定理即可求出所成角的余 弦值. 【详解】设正方体 的棱长为 ， 与正方体 的每条棱所成角都相等的直线为其体对角线所在直线， 求此直线与 所成角的余弦值即求 的余弦值， 可知 ， ， ， ABCD AB 2 2 1 1 1 1ABCD A B C D− AB 2 2 3 3 3 2 6 3 1 1 1 1ABCD A B C D− a 1 1 1 1ABCD A B C D− AB 1C AB∠ AB a= 1 2BC a= 1 3AC a= - 8 - 有 ， 故此直线与 所成角的余弦值为 . 故选：B. 【点睛】本题主要考查了几何体中线线的夹角问题，属于简单题. 12.已知 是数列 的前 项和， ，通过计算得 ， ， ， ，根据通项的规律可以归纳得出 （ ） A. 981 B. 979 C. 980 D. 978 【答案】A 【解析】 【分析】 通过计算 ， ， ， 的式子特点，归纳出 的通项公式，进而可求 . 【详解】由 可以猜想， 的通项公式均为关于 的多 项式，且 中 的次数最高次为 4 次，则 中 的次数最高次为 3 次， 则 ， ， ， ， ， ， ， ， ∴根据通项的规律可以归纳得出 . 故 . 故选：A. 【点睛】本题考查观察法求数列的通项公式，考查学生观察能力和计算能力. 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13.对奇数列 1，3，5，7，9…，进行如下分组：第一组含一个数 ；第二组含两个数 ； 2 2 2 1 2 3 2 3cos 32 3 a a aC AB a + −∠ = = AB 3 3 nS { }na n ( )2 24 3 3 2 1n na S n n n n+ = + − − + 1 0a = 2 5a = 3 22a = 4 57a = 10a = 1a 2a 3a 4a { }na 10a ( )2 24 3 3 2 1n na S n n n n+ = + − − + ,n na S n nS n na n 3 11 2 1 1a− = × − 3 1 1 2 1 1 0a = − × + = 3 22 2 2 1a− = × − 3 2 2 2 2 1 5a = − × + = 3 33 2 3 1a− = × − 3 3 3 2 3 1 22a = − × + = 3 44 2 4 1a− = × − 3 4 4 2 4 1 57a = − × + = 3 2 1na n n= − + 10 981a = { }1 { }3,5 - 9 - 第三组含三个数 ；第四组含四个数 ；…试观察猜想每组内各数之和 ( )与组的编号数 的关系式为________． 【答案】 【解析】 【分析】 先求出 ， ， ， 的值，再归纳出 即可. 【 详 解 】 解 ： 观 察 前 四 组 数 个 数 之 和 可 得 ， ， ， ， ，…， 则猜想第 组各数之和等于 ， 故答案为： ． 【点睛】本题考查了归纳推理能力，重点考查了对数据的分析处理能力，属基础题. 14.两个线性相关变量 满足如下关系: 则 与 的线性回归直线 一定过其样本点的中心，其坐标为_________________． 【答案】 【解析】 【分析】 根据表中数据求出变量 ， 的平均值，即求出了样本的中心点. 【详解】线性回归直线 的样本点中心为点 ， 因为 ， ， 所以该线性回归直线的样本点中心为点 . 故答案为： . { }7,9,11 { }13,15,17,19 ( )f n *n∈N n 3( )f n n= (1)f (2)f (3)f (4)f ( )f n 3(1) 1 1f = = 3(2) 3 5 8 2f = + = = 3(3) 7 9 11 27 3f = + + = = 3(4) 13 15 17 19 64 4f = + + + = = n 3n 3( )f n n= ,x y x 2 4 5 6 8 y 2.2 4.3 4.8 6.5 7.2 y x y bx a= + ( )5,5 x y y bx a= + ( ),x y 2 4 5 6 8 55x + + + += = 2.2 4.3 4.8 6.5 7.2 55y + + + += = ( )5,5 ( )5,5 - 10 - 【点睛】本题主要考查了线性回归方程过样本中心点的性质，属于基础题. 15.下面是一个 列联表: 总计 总计 其中 处填的值分别为________________． 【答案】 ， 【解析】 【分析】 根据联表的性质，首先求出 ， 的值即可. 【详解】由 ，得 ， ，得 . 故答案为： ， . 【点睛】本题主要考查了联表中数据的性质，属于基础题. 16.某企业对 4 个不同的部门的个别员工的年旅游经费调查发现，员工的年旅游经费 （单位 ：万元）与其年薪（单位：万元）有较好的线性相关关系，通过下表中的数据计算得到 关 于 的线性回归方程为 . 7 10 12 15 0.4 1.1 1.3 2.5 那么，相应于点 的残差为_______． 【答案】0.0284 【解析】 2 2× 1y 2y 1x 35 a 70 2x 15 15 30 50 b 100 ,a b 35 50 a b 35 70a + = 35a = 15a b+ = 50b = 35 50 y y x  0.2529 1.4574y x= − x y (10,1.1) - 11 - 【分析】 将 x=10 代入线性回归方程，求得 ，利用残差公式计算即可. 【详解】当 时， ， ∴残差为 y- . 故答案为 . 【点睛】本题考查了线性回归方程的应用问题，考查了残差的计算公式，是基础题． 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17.《朗读者》是一档文化情感类节目，以个人成长、情感体验、背景故事与传世佳作相结合 的方式，选用精美的文字，用最平实的情感读出文字背后的价值，深受人们的喜爱.为了了解 人们对该节目的喜爱程度，某调查机构随机调查了 ， 两个城市各 100 名观众，得到下面 的列联表. 非常喜爱 喜爱 合计 城市 60 100 城市 30 合计 200 完成上表，并根据以上数据，判断是否有 的把握认为观众的喜爱程度与所处的城市有关？ 附参考公式和数据： （其中 ）. 0.15 0.10 0.05 0.025 0.010 2.072 2.706 3.841 5.024 6.635 【答案】列表见解析，没有 的把握认为观众的喜爱程度与所处的城市有关 【解析】 【分析】 ˆy 10x = 1. 16ˆ 07y = 1.1 1.0716 0.0284ˆy = − = 0.0284 A B A B 90% ( ) ( )( )( )( ) 2 2 n ad bcK a b c d a c b d −= + + + + n a b c d= + + + ( )2 0P K k≥ 0k 90% - 12 - 由题意填写列联表，根据公式计算观测值，对照临界值得出结论即可. 【详解】完成 列联表如下 非常喜爱 喜爱 合计 城市 60 40 100 城市 70 30 100 合计 130 70 200 的观测值 ， 所以没有 的把握认为观众的喜爱程度与所处的城市有关. 【点睛】本题考查了独立性检验的问题，是基础题. 18.已知 ， ，求证: .（分别用综合法、分析法证明） 【答案】证明见解析 【解析】 【分析】 综合法首先利用基本不等式转化原不等式，再结合 ， 即可得证；分析 法需要构造出平方和，通过平方和大于零证明不等式 【详解】综合法: ， ， ， 又 ， ， ， ； . 2 2× A B 2K ( ) ( )( )( )( ) ( )2 2200 40 70 30 60 200 2.198 2.706100 100 130 70 91 n ad bck a b c d a c b d − × − ×= = = ≈ <+ + + + × × × 90% 2 2 1a b+ = 2 2 1x y+ = 1ax by+ ≤ 2 2 1a b+ = 2 2 1x y+ = 2 22ax a x≤ + 2 22by b y≤ + ( ) ( ) ( )2 2 2 22 ax by a b x y∴ + ≤ + + + 2 2 1a b + = 2 2 1x y+ = ( )2 2ax by∴ + ≤ 1ax by∴ + < - 13 - 分析法:要证 成立， 只要证 ， 只要证 ， 又 ， ， 只要证 ， 即证 显然成立， . 【点睛】本题主要考查了利用分析法和综合法证明不等式，注意 的妙用，属于一般题. 19.已知若椭圆 ： （ ）交 轴于 ， 两点，点 是椭圆 上异于 ， 的任意一点，直线 ， 分别交 轴于点 ， ，则 为定值 . （1）若将双曲线与椭圆类比，试写出类比得到的命题； （2）判定（1）类比得到命题的真假，请说明理由. 【答案】（1）见解析；（2）命题为真命题，证明见解析. 【解析】 【分析】 （1）根据类比推理的基本原则可直接写出结果； （2）设 ， ， ，表示出直线 方程后可求得 点坐标，由此得 到 ，同理得到 ，根据平面向量的数量积运算可构造方程，结合点 在双曲线上可化 简得到结果. 【详解】（1）类比得命题：若双曲线 ： 交 轴于 两点，点 是双曲线 上异于 的任意一点，直线 分别交 轴于点 ，则 为定 值 . （2）在（1）中类比得到的命题为真命题，证明如下： 1ax by+ ≤ ( )1 0ax by− + ≥ 2 2 2 0ax by− − ≥ 2 2 1a b + = 2 2 1x y+ = 2 2 2 2 2 2 0a b x y ax by+ + + − − ≥ ( ) ( )2 2 0a x b y− + − ≥ 1ax by∴ + < 1 C 2 2 2 2 1x y a b + = 0a b> > x A B P C A B PA PB y M N AN BM⋅  2 2b a− ( ),0A a− ( ),0B a ( )0 0,P x y PA M BM AN P C ( )2 2 2 2 1 0, 0x y a ba b − = > > x ,A B P C ,A B ,PA PB y ,M N AN BM⋅  ( )2 2a b− + - 14 - 不妨设 ， ， ，则 ， ∴直线 方程为 . 令 ，则 ，∴点 坐标为 . 又 ，∴ . 同法可求得： . ∴ . 又∵ ，∴ . 【点睛】本题考查类比推理的应用、双曲线中定值问题的证明；关键是能够熟练应用直线与 双曲线的相关知识，表示出所需的平面向量，根据平面向量数量积的坐标运算可化简得到结 果. 20.每年 10 月中上旬是小麦 最佳种植时间，但小麦的发芽会受到土壤、气候等多方面因素 的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系，在不同的温差下统 计了 100 颗小麦种子的发芽数，得到了如下数据： 温差 8 10 11 12 13 发芽数 （颗） 79 81 85 86 90 （1）请根据统计的最后三组数据，求出 关于 的线性回归方程 ； （2）若由（1）中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗， 则认为线性回归方程是可靠的，试判断（1）中得到的线性回归方程是否可靠； （3）若 100 颗小麦种子的发芽率为 颗，则记为 的发芽率，当发芽率为 时，平均每 亩地的收益为 元，某农场有土地 10 万亩，小麦种植期间昼夜温差大约为 ，根据（1） 的 ( ),0A a− ( ),0B a ( )0 0,P x y ( )0 0 0 0 0 PA y yk x a x a −= =− − + PA ( )0 0 yy x ax a = ++ 0x = 0 0 ayy x a = + M 0 0 0, ay x a    +  ( ),0B a 0 0 , ayBM a x a  = − +   0 0 , ayAN a x a  −=  −   2 2 2 0 2 2 0 a yAN BM a x a ⋅ = − − −   2 2 0 0 2 2 1x y a b − = ( )22 2 2 2 20 2 2 2 0 1xaAN BM a b a bx a a   ⋅ = − − ⋅ ⋅ − = − +  −      ( )x C° y y x y bx a= +   n %n %n 10n 9 C° - 15 - 中得到的线性回归方程估计该农场种植小麦所获得的收益. 附：在线性回归方程 中， . 【答案】（1） （2）见解析（3）7950 万元 【解析】 【分析】 （1）先进行数据处理：每个温差值减去 12，每个发芽数减去 86，得到新的数据表格，求出 的值，最后求出 关于 的线性回归方程 ； （2）根据线回归方程，分别计算当 时，当 时，它们的估计值，然后判断（1）中 得到的线性回归方程是否可靠； （3）当 时，根据线性回归方程计算出 的值，然后计算出发芽率以及收益. 【详解】数据处理 ； . （1） -1 0 1 -1 0 4 此时： ， ， ， ， ∴ ，∴ . （2）当 时： ， 符合， 当 时： ， 符合， 前两组数据均符合题意，该回归直线方程可靠. （3）当 时， . y bx a= +   1 22 1 n i i i n i i x y nxy b x nx = = − = − ∑ ∑  5 572 ˆy x= + 11 ˆ, , ,ˆy bx a， y x y bx a= +   8x = 10x = 9x = ˆy 12x − 86y − x 12x − y 86y − 1 0x = 1 1y = 1 4 3 0 1 5 1 1 3 0 2 ˆb + − × ×= =+ − × 1 1 ˆˆ 51 0 12a y b x= − ⋅ = − × = 586 ( 12)2 ˆ 1y x− = − + 5 572 ˆy x= + 8x = ˆ 77y = 79 77 2 2− = ≤ 10x = ˆ 82y = 82 81 1 2− = ≤ 9x = ˆ 79.5y = - 16 - 发芽率 ，∴ . 收益： （万亩） （万元）. 种植小麦收益为 7950 万元. 【点睛】本题考查了求线性回归方程，以及用数据检验线性回归方程是否可靠，考查了应用 线性回归方程估计收益问题，考查了数学应用能力. 21.已知函数 . （1）证明:函数 不存在小于 的零点； （2）证明:当 时， 的最小值为 . 【答案】（1）证明见解析；（2）证明见解析. 【解析】 【分析】 （1）利用反证法证明函数 在 时无零点即可； （2）首先对函数 求导，证明函数 的单调性，根据单调性求出函数 在区间 上的最小即可. 【详解】（1）假设存在 使 成立， 所以存在 使 成立，因为 ， 所以 ， 而 与 相矛盾，故假设不成立， 所以函数 不存在小于 的零点； （2）因为 ，所以 ， 令 ，有 ， 令 ，则 ， 可知当 时， ，当 时， ， 79.5% 79.5%100n = = 79.5n = 79.5 10 10× × 7950= ( ) ( )1 2xf x x e x= + + − ( )f x 0 [ 3, )x∈ − +∞ ( )f x -32 5e− − ( )f x 0 ),( 0x ∈ ∞- ( )f x ( )f x ( )f x [ 3, )− +∞ 0 ),( 0x ∈ ∞- ( ) 0 0 01 2 0xx e x+ − =+ 0 ),( 0x ∈ ∞- 0 0 0 2 1 x xe x −− += 0 0x < 00 1xe< < ⇒ 0 0 20 11 x x −< − < − ⇒+ 0 1 22 x< < 0 1 22 x< < 0 0x < ( )f x 0 ( ) ( )1 2xf x x e x= + + − ( ) ( )2 1xf x x e′ = + + ( ) ( )2 1xg x x e= + + ( ) ( )3 xg x x e′ = + ( ) 0g x′ = 3x = − 3x < − ( ) 0g x′ < 3x > − ( ) 0g x′ > - 17 - 所以函数 在区间 上单调递减，在区间 上单调递增， 所以 ， 所以 对任意 恒成立， 所以函数 在区间上 单调递增， 所以当 时， . 【点睛】本题主要考查了函数的值域求解，利用导数求解函数的最值，属于一般题. 22.已知数列 满足 ， . （1）求 ； （2）若 证明:数列 中的任意三项不可能构成等差数列. 【答案】（1） ；（2）证明见解析. 【解析】 【分析】 （1）首先设参数 构造等比数列，求出等比数列的通项公式，即可求出求 ； （2）首先求出数列 的通项公式，然后根据等差中项证明等差数列是否成立即可. 【详解】（1）据题意设 ，所以 ， 又因为 ，所以 ，有 ， 故数列 是以 为首项， 为公比的等比数列， 所以 ， 整理得 ； ( )g x ( , 3)−∞ − ( 3, )− +∞ ( ) ( ) 3 3( )3 3 2 1 1 0ming x g e e− −= − = − + + = − + > ( ) 0f x′ > x∈R ( )f x ( , )−∞ +∞ [ 3, )x∈ − +∞ ( ) ( ) 3 33 2 3 2 2 5minf x f e e− −= − = − − − = − − { }na 1 1 2a = 2 2 1 2 1 3 3n na a+ = + 2 na 2 2 1 ,n n nb a a+= − { }nb 1 2 3 21 4 3 n na − = − ⋅   t 2 na { }nb ( )2 2 1 2 3n na t a t+ + = + 2 2 1 2 1 3 3n na a t+ = − 2 2 1 2 1 3 3n na a+ = + 1t = − ( )2 2 1 21 13n na a+ − = − { }2 1na − 2 1 31 4a − = − 2 3 1 2 3 21 4 3 n na − − = − ⋅   1 2 3 21 4 3 n na − = − ⋅   - 18 - （2）由（1）有 ，所以 ， 假设数列 中存在三项 ， ， ， 按某种顺序构成等差数列， 因为数列 是首项为 ，公比为 的等比数列，所以 ， 所以只能有 成立， 即 ， 化简得 ， 因为 ，所以 为奇数， 为偶数， 故 不可能成立，即假设不成立， 故数列 中任意三项不可能构成等差数列. 【点睛】本题主要考查了构造等比数列求数列通项，证明数列是否为等差数列，属于一般题. 1 2 3 21 4 3 n na − = − ⋅   1 2 2 1 1 2 4 3 n n n nb a a − +  = − =    { }nb rb sb tb ( )r s t< < { }nb 1 4 2 3 r s tb b b> > 2 s r tb b b= + 1 1 11 2 1 2 1 22 4 3 4 3 4 3 s r t− − −     × × = × + ×           3 2 2 2 3t r t r s r t s− − − −+ = × × r s t< < 3 2t s t r− −+ 2 2 3s r t s− −× × 3 2 2 2 3t r t r s r t s− − − −+ = × × { }nb - 19 -