云南省昆明市2020届高三“三诊一模”高考模拟考试（三模）数学（理）试题 Word版含解析 26页

昆明市2020届“三诊一模”高考模拟考试 理科数学 注意事项：‎ ‎1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上，并认真核准条形码上的准考证号、姓名、考场号、座位号及科目，在规定的位置贴好条形码．‎ ‎2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．‎ ‎3．考试结束后，将本试卷和答题卡交回．‎ 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.在复平面内，复数所对应的点位于（ ）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用复数代数形式的乘除运算化简，求出的坐标得答案．‎ ‎【详解】解：，‎ 复数所对应的点的坐标为，位于第一象限．‎ 故选：．‎ ‎【点睛】本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，属于基础题．‎ ‎2.已知集合，，则（ ）．‎ A. B. C. D. 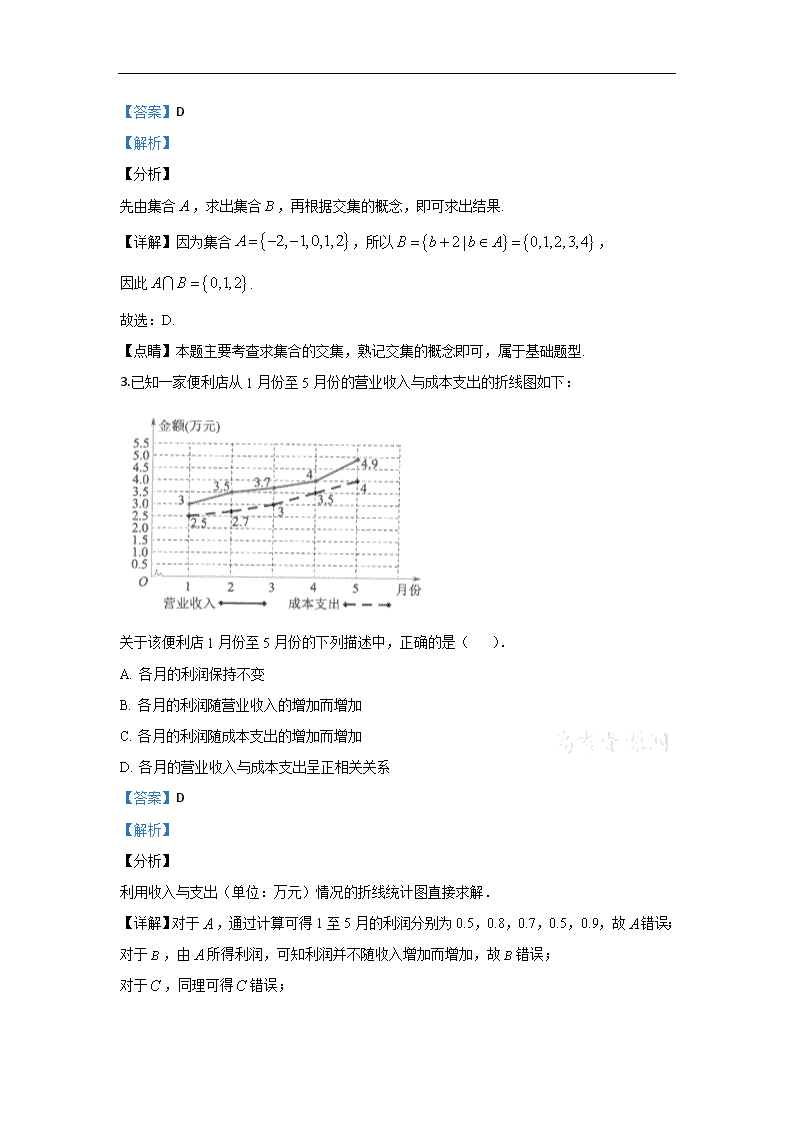‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 先由集合，求出集合，再根据交集的概念，即可求出结果.‎ ‎【详解】因为集合，所以，‎ 因此.‎ 故选：D.‎ ‎【点睛】本题主要考查求集合的交集，熟记交集的概念即可，属于基础题型.‎ ‎3.已知一家便利店从1月份至5月份的营业收入与成本支出的折线图如下：‎ 关于该便利店1月份至5月份的下列描述中，正确的是（ ）．‎ A. 各月的利润保持不变 B. 各月的利润随营业收入的增加而增加 C. 各月的利润随成本支出的增加而增加 D. 各月的营业收入与成本支出呈正相关关系 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用收入与支出（单位：万元）情况的折线统计图直接求解．‎ ‎【详解】对于，通过计算可得1至5月的利润分别为0.5，0.8，0.7，0.5，0.9，故错误；‎ 对于，由所得利润，可知利润并不随收入增加而增加，故错误；‎ 对于，同理可得错误；‎ 对于，由折线图可得支出越多，收入也越多，故而收入与支出呈正相关，故正确，‎ 故选：D．‎ ‎【点睛】本题考查学生合情推理的能力，考查折线统计图的性质等基础知识，考查运算求解能力，考查数形结合思想，是基础题．‎ ‎4.已知点在双曲线的一条渐近线上，该双曲线的离心率为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据点在双曲线的一条渐近线上可得的关系，再根据求解即可.‎ ‎【详解】由题，点在直线上，即，故离心率.‎ 故选：C ‎【点睛】本题主要考查了双曲线的离心率求解，需要根据题意确定的关系，进而求得离心率.属于基础题.‎ ‎5.已知点，，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 利用两点间距离公式结合三角函数公式求解．‎ ‎【详解】点，，‎ ‎，‎ 故选：B．‎ ‎【点睛】本题主要考查了两点间距离公式，以及三角函数公式，是基础题．‎ ‎6.如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体的体积为（ ）‎ A. 216 B. 108 C. D. 36‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 首先把三视图转换为几何体，进一步求出三棱柱体的体积．‎ ‎【详解】根据几何体的三视图转换为直观图为：该几何体为底面为等腰三角形，高为6的三棱柱体，‎ 如图所示：‎ 所以：．‎ 故选：B．‎ ‎【点睛】本题考查的知识要点：三视图和直观图形之间的转换，几何体的体积公式的应用，主要考查学生的运算能力和转换能力及思维能力．‎ ‎7.材料一：已知三角形三边长分别为，，，则三角形的面积为，其中．这个公式被称为海伦-秦九韶公式 材料二：阿波罗尼奥斯（Apollonius）在《圆锥曲线论》中提出椭圆定义：我们把平面内与两个定点，的距离的和等于常数（大于）的点的轨迹叫做椭圆．‎ 根据材料一或材料二解答：已知中，，，则面积的最大值为（ ）‎ A. B. 3 C. D. 6‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据材料二可得点的轨迹为椭圆，当点运动到椭圆短轴的顶点时，可得的面积取得最大值.‎ ‎【详解】由材料二可得点的轨迹为椭圆，其焦距，长轴，短轴 当点运动到椭圆短轴的顶点时，可得的面积取得最大值，‎ ‎，‎ 故选：C.‎ ‎【点睛】本题考查椭圆的定义及三角形面积的最值，考查数形结合思想，考查运算求解能力.‎ ‎8.已知函数的图象向左平移个单位后与的图象重合，则的最小值为（ ）‎ A. 8 B. 4 C. 2 D. 1‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据题意，得到为函数周期的整数倍，进而可得出结果.‎ ‎【详解】因为函数的图象向左平移个单位后与的图象重合，‎ 所以（其中为函数的最小正周期），‎ 即，所以，因为，所以.‎ 故选：B.‎ ‎【点睛】本题主要考查由三角函数的周期求参数的问题，属于基础题型.‎ ‎9.如图1，已知是直角梯形，∥，，在线段上，．将沿折起，使平面平面，连接，，设的中点为，如图2．对于图2，下列选项错误的是（ ）‎ A. 平面平面 B. 平面 C D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用线面垂直判定与性质进行证明平面,，证明是直角三角形可得.‎ ‎【详解】由已知是直角梯形，∥，， ‎ 得四边形是矩形，所以∥,, ‎ ‎， 所以平面,‎ 又∥,平面,所以B正确 平面平面,平面平面,‎ 平面，平面,所以C正确 平面,又,‎ 平面,,是直角三角形，又的中点为 所以，所以D正确.‎ 故选：A ‎【点睛】求解翻折问题的关键及注意事项：‎ 求解平面图形翻折问题的关键是弄清原有的性质变化与否，即翻折(转)后还在同一个平面上的性质不发生变化，不在同一个平面上的性质发生变化．应注意：‎ ‎(1)点的变化，点与点的重合及点的位置变化；‎ ‎(2)线的变化，翻折(转)前后，若线始终在同一平面内，则它们的位置关系不发生变化，若线与线由在一个平面内转变为不在同一个平面内，应注意其位置关系的变化；‎ ‎(3)长度、角度等几何度量的变化．‎ ‎10.已知为抛物线的焦点，点为抛物线上一点，以线段为直径的圆与轴相切于点，且满足，，则的值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 作出图形，根据题意推导出轴，结合，可得出点的坐标，再将点的坐标代入抛物线的方程，可求得正数的值.‎ ‎【详解】如下图所示，设线段的中点为点，‎ 由题意可知，圆与轴相切于点，则轴，‎ 又，为的中点，，轴，‎ 由于，则点，将点的坐标代入抛物线方程得，即，‎ ‎，解得.‎ 故选：C.‎ ‎【点睛】本题考查抛物线方程中参数的求解，根据题意求出点的坐标是解题的关键，考查计算能力，属于中等题.‎ ‎11.已知函数，是的唯一极小值点，则实数的取值范围为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 求导可得，再根据是的唯一极小值点可得恒成立，再根据恒成立问题求解最小值分析即可.‎ ‎【详解】求导有.‎ 设，则，‎ 故当时，单调递减；时，单调递增.‎ 故若有两个零点，则必有一根，则此时有时；时，故为的极小值点，与题意不符.‎ 故恒成立，故，即，解得 ‎.‎ 故选：D ‎【点睛】本题主要考查了根据导数求解极值点的问题，需要根据极值点满足的关系分析得导函数零点的个数，再求最值求解参数的范围，属于中档题.‎ ‎12.中，，，有下述四个结论：‎ ‎①若为的重心，则 ‎②若为边上的一个动点，则为定值2‎ ‎③若，为边上的两个动点，且，则的最小值为 ‎④已知为内一点，若，且，则的最大值为2‎ 其中所有正确结论的编号是（ ）‎ A. ①③ B. ①④ C. ②③ D. ②④‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据题意，先得为等腰直角三角形；①取中点为，连接，得到，根据平面向量基本定理，即可得出结果；②先由①得到，由题意得到在上的投影为，进而可求出向量数量积；③以点为坐标原点，分别以、所在直线为轴、轴，建立平面直角坐标系，由题意，设，且，不妨令，根据向量数量积的坐标表示，即可求出结果；④同③建立平面直角坐标系，设，根据题意，得到，再设，由题意，得到，，用表示出，即可求出结果；‎ ‎【详解】因为在中，，； 所以为等腰直角三角形；‎ ‎①如图1，取中点为，连接，因为为的重心，‎ 所以在上，且，‎ 所以，故①正确；‎ ‎②如图1，同①，因为为中点，为等腰直角三角形，所以，‎ 若为边上的一个动点，则在上的投影为，‎ 因此，故②错；‎ ‎③如图2，以点为坐标原点，分别以、所在直线为轴、轴，建立如图所示的平面直角坐标系，则，，，易得，所在直线方程为：；‎ 因为，为边上的两个动点，‎ 所以设，，且，不妨令，‎ 因为，所以，即，则，‎ 所以 ‎，当且仅当时，等号成立；故③正确；‎ ‎④同③建立如图3所示的平面直角坐标系，则，，‎ 设，则，‎ 又，所以，即 因为为内一点，且，设，‎ 则，且，，‎ 因此，‎ 因为，所以，所以无最值，即无最值，故④错.‎ 故选：A.‎ ‎【点睛】本题主要考查平面向量基本定理的应用，以及求平面向量的数量积等问题，熟记平面向量基本定理，灵活运用建系的方法求解即可，属于常考题型.‎ 二、填空题：本題共4小题，每小题5分，共20分．‎ ‎13.若，则__________．‎ ‎【答案】10‎ ‎【解析】‎ ‎【分析】‎ 首先写出展开式的通项，即可求出含的项的系数；‎ ‎【详解】解：因为，的展开式的通项为 ‎，令，得，则 故 故答案为：10‎ ‎【点睛】本题考查二项式定理的应用，属于基础题.‎ ‎14.若“，”是真命题，则实数的取值范围是__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据对数函数的性质得到关于的不等式，解出即可．‎ ‎【详解】解： “”是真命题，‎ ‎；‎ 故答案为：．‎ ‎【点睛】本题考查了特称命题的真假，考查对数函数的性质，属于基础题．‎ ‎15.在中，，，，在线段上，若与的面积之比为，则__________．‎ ‎【答案】1‎ ‎【解析】‎ ‎【分析】‎ 由与的面积之比为，可得，进而求得，在用余弦定理即可求得.‎ ‎【详解】解：如图，‎ 因为与的面积之比为，‎ 所以，又因为，所以，‎ 在中，由余弦定理得，‎ 所以.‎ 故答案为：1.‎ ‎【点睛】本题主要考查用余弦定理来解三角形，考查学生的计算能力和公式得掌握程度，属于基础题.‎ ‎16.某校同时提供、两类线上选修课程，类选修课每次观看线上直播分钟，并完成课后作业分钟，可获得积分分；类选修课每次观看线上直播分钟，并完成课后作业分钟，可获得积分分．每周开设次，共开设周，每次均为独立内容，每次只能选择类、类课程中的一类学习．当选择类课程次，类课程次时，可获得总积分共_______分．如果规定学生观看直播总时间不得少于分钟，课后作业总时间不得少于分钟，则通过线上选修课的学习，最多可以获得总积分共________分．‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【分析】‎ 根据题意可计算出当选择类课程次，类课程次时，可获得的总积分；设学生选择类选修课次，类选修课次，根据题意列出有关、的约束条件，可得出目标函数为，利用线性规划思想可求得的最大值，进而得解.‎ ‎【详解】根据题意，当选择类课程次，类课程次时，可获得总积分分.‎ 设学生选择类选修课次，类选修课次，‎ 则、所满足的约束条件为，即，目标函数为，如下图所示：‎ 则可行域为图中阴影部分中的整数点（横坐标和纵坐标均为整数的点），‎ 联立，解得，可得点，‎ 平移直线，当直线经过可行域的顶点时，直线在轴上的截距最大，此时取最大值，即.‎ 因此，通过线上选修课的学习，最多可以获得总积分共分.‎ 故答案为：；.‎ ‎【点睛】本题考查线性规划的实际应用，将问题转化为线性规划问题是解答的关键，考查数形结合思想的应用，属于中等题.‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题：共60分．‎ ‎17.已知数列为正项等比数列，为的前项和，若，．‎ ‎（1）求数列的通项公式；‎ ‎（2）从三个条件：①；②；③‎ 中任选一个作为已知条件，求数列的前项和．‎ 注：如果选择多个条件分别解答，按第一个解答计分．‎ ‎【答案】（1）（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎(1)设数列的公比为，再根据题意利用基本量法求解即可.‎ ‎(2) 选择①可得，即可利用等比数列求和公式求解即可.‎ 选择②可得，再根据等比与等差数列求和的公式求解即可.‎ 选择③可得，再用等差数列求和公式求解即可.‎ ‎【详解】解：‎ ‎（1）设数列的公比为，因为：，所以，故：，‎ 解得：或（舍去），故． ‎ 由：，得：，将代入得：，‎ 所以数列的通项公式为：； ‎ ‎（2）选择①：‎ ‎，‎ 数列是首项为，公比为的等比数列， ‎ 所以，‎ 选择②：‎ ‎， ‎ 所以 ‎ 选择③：‎ ‎，‎ 数列是首项为0，公差为1的等差数列． ‎ 所以．‎ ‎【点睛】本题主要考查了等比数列的基本量求解，同时也考查了等差等比数列求和的公式，属于基础题.‎ ‎18.已知四棱锥中，底面是边长为4的正方形，为正三角形，是的中点，过的平面平行于平面，且平面与平面的交线为，与平面的交线为．‎ ‎（1）在图中作出四边形（不必说出作法和理由）；‎ ‎（2）若，求平面与平面形成的锐二面角的余弦值．‎ ‎【答案】（1）见解析（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）四边形MNOE即为所求，其中N为PD中点，O为AD中点，E为BC中点；‎ ‎（2）连结OP，推导出，，平面PAD，，从而平面ABCD，，，，以O为原点，建立空间直角坐标系，利用向量能求出平面与平面PBC形成的锐二面角的余弦值.‎ ‎【详解】（1）如图，四边形即为所求，其中为中点，为中点，为中点；‎ ‎（2）连接，依题意：，‎ 所以，则，‎ 又因为且，‎ 所以平面，则，‎ 因为为正三角形且为中点，‎ 所以平面，‎ 则，，，‎ 以为原点建立如图坐标系， ‎ 因为，所以，，，，‎ 则，，， ‎ 设平面的一个法向量为，则 ‎，解得，‎ 设平面的一个法向量为，‎ 则，解得．‎ 则， ‎ 所以平面与平面形成的锐二面角的余弦值为.‎ ‎【点睛】本题考查平面的作法，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间思维能力，属于中档题.‎ ‎19.已知椭圆左焦点为，经过点的直线与圆相交于，两点，是线段与的公共点，且．‎ ‎（1）求椭圆的方程；‎ ‎（2）与的交点为，，且恰为线段的中点，求的面积．‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据椭圆的定义可求得，又，故，由此可得的方程；‎ ‎（2）根据为线段的中点，得，由以及可得的坐标，从而可得三角形的面积.‎ ‎【详解】（1）如图：‎ 由圆可得， ‎ 因为，‎ 所以，‎ 即，又，故， ‎ 所以椭圆的方程为．‎ ‎（2）设，，易知，‎ 因为为线段的中点，则， ‎ 所以，‎ 又，解得，，‎ 若，则，直线的方程为，‎ 由，消去得，所以，所以，，即，‎ 所以的面积．‎ 若，同理可求得的面积．‎ 综上，的面积为.‎ ‎【点睛】本题考查了根据椭圆的定义求椭圆方程，考查了圆的性质，考查了两个垂直向量的坐标表示，考查了直线与椭圆的交点，考查了三角形的面积公式，属于中档题.‎ ‎20.近年来，国家为了鼓励高校毕业生自主创业，出台了许多优惠政策，以创业带动就业．某高校毕业生小张自主创业从事苹果的种植，并开设网店进行销售．为了做好苹果的品控，小张从自己果园的苹果树上，随机摘取150个苹果测重（单位：克），其重量分布在区间内，根据统计的数据得到如图1所示的频率分布直方图．‎ ‎（1）以上述样本数据中频率作为概率，现一顾客从该果园购买了30个苹果，求这30个苹果中重量在内的个数的数学期望；‎ ‎（2）小张的网店为了进行苹果的促销，推出了“买苹果，送福袋”的活动，买家在线参加按图行进赢取福袋的游戏．该游戏的规则如下：买家点击抛掷一枚特殊的骰子，每次抛掷的结果为1或2，且这两种结果的概率相同；从出发格（第0格）开始，每掷一次，按照抛掷的结果，按如图2所示的路径向前行进一次，若掷出1点，即从当前位置向前行进一格（从第格到第格，），若掷出2点，即从当前位置向前行进两格（从第格到第格，），行进至第3l格（获得福袋）或第32格（谢谢惠顾），游戏结束．设买家行进至第格的概率为，．‎ ‎（ⅰ）求、，并写出用、表示的递推式；‎ ‎（ⅱ）求，并说明该大学生网店推出的此款游戏活动，是更有利于卖家，还是更有利于买家．‎ ‎【答案】（1）8.4个；（2）（ⅰ）,．（ⅱ），更有利于买家．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据频率分布直方图可求出苹果的重量在 内的频率，再根据二项分布的期望公式可得结果；‎ ‎ （2）（ⅰ）由当前格在第0格，且第一次抛掷骰子，结果为1，可求得；由当前格在第0格，第一次抛掷骰子，结果为2，和当前格在第1格，第二次抛掷骰子，结果为1，这两个互斥事件的和事件的概率公式可求得；分两种情况可求得：①当前格在第格，抛掷一次骰子，结果为2，②当前格在第格，抛掷一次骰子，结果为1，‎ ‎（ii）根据（ⅰ）的递推关系可求得，由此可得，根据可求得，再比较大小可得答案.‎ ‎【详解】（1）由图可知，苹果的重量在内的频率为：．‎ 一顾客从该果园购买的30个苹果中重量在内的个数为，则，所以（个）．‎ ‎（2）（i）买家要行进至第1格的情况只有一种：买家第一次抛掷骰子，结果为1，行进至第一格，其概率为，则； ‎ 买家要行进至第2格的情况有以下两种：‎ ‎①当前格在第0格，第一次抛掷骰子，结果为2，行进至第2格，其概率为；‎ ‎②当前格在第1格，第二次抛掷骰子，结果为1，行进至第2格，其概率为；‎ 所以． ‎ 买家要行进至第格的情况有以下两种：‎ ‎①当前格在第格，抛掷一次骰子，结果为2，行进至第格，其概率为；‎ ‎②当前格在第格，抛掷一次骰子，结果为1，行进至第格，其概率为；‎ 所以． ‎ ‎（ii）由（i）得，，即，‎ 又，‎ 所以数列是首项为，公比为的等比数列．‎ 所以，‎ 所以 ‎，‎ 即．‎ 所以买家行进至第31格（获得福袋）的概率为；‎ 又买家行进至第32格（谢谢惠顾）的概率为，‎ 由于，‎ 所以买家行进至第31格的概率大于行进至第32格的概率，即小张网店推岀的此款游戏活动是更有利于买家．‎ ‎【点睛】本题考查了由频率分布直方图求频率，考查了二项分布的期望公式，考查了由递推关系求数列的通项，属于中档题.‎ ‎21.已知，，．‎ ‎（1）若，证明：；‎ ‎（2）对任意，都有，求整数的最大值．‎ ‎【答案】（1）见解析（2）2‎ ‎【解析】‎ ‎【分析】‎ ‎（1）构造函数，利用二次求导可证明结论成立；‎ ‎（2）利用时，不等式成立以及（1）结论，可得，从而只需证明在区间恒成立即可．再根据（1）的结论，转化为证明在上恒成立.利用导数即可证明，由此可得结果.‎ ‎【详解】（1）设，则，‎ 因为，且，‎ 则在单调递减，因为，，‎ 所以存在唯一零点，使得，‎ 所以时，，时，，‎ 则在时单调递增，在上单调递减，‎ 又，，‎ 所以在上恒成立，所以在上单调递增，‎ 则，即．‎ 所以． ‎ ‎（2）因为对任意的，不等式，‎ 即恒成立，‎ 令，则，‎ 由（1）知，所以，‎ 由于为满足的整数，则， ‎ 因此．‎ 下面证明在区间恒成立即可．‎ 由（1）知，则，‎ 故，‎ 设，，则，‎ 所以在上单调递减，‎ 所以，所以在上恒成立．‎ 综上所述，的最大值为2．‎ ‎【点睛】本题考查了构造函数并利用导数证明不等式成立，考查了利用导数处理不等式恒成立问题，考查了零点存在性定理，多次构造函数求导，利用放缩法进行转化是本题的难点，属于难题.‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答．并用铅笔在答题卡选考题区域内把所选的题号涂黑．如果多做，则按所做的第一题计分．‎ ‎[选修4-4：坐标系与参数方程]‎ ‎22.在平面直角坐标系中，直线过点，倾斜角为．以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程．‎ ‎（1）写出直线的参数方程及曲线的直角坐标方程；‎ ‎（2）若与相交于，两点，为线段的中点，且，求．‎ ‎【答案】（1）直线的参数方程为（为参数）， 曲线的直角坐标方程为 ‎．（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据点，倾斜角为可得直线的参数方程，两边同时乘以后，根据互化公式可得曲线的直角坐标方程；‎ ‎（2）将直线的参数方程代入抛物线方程，利用参数的几何意义可解得结果.‎ ‎【详解】（1）根据直线过点，倾斜角为可得直线的参数方程为（为参数），‎ 由得，将，代入可得 曲线直角坐标方程：.‎ ‎（2）将，代入到，得，‎ 设对应的参数分别为，则对应的参数为，‎ 由韦达定理得，所以，‎ 所以，所以，‎ 所以，解得，‎ 由，所以.‎ ‎【点睛】本题考查了直线的参数方程及其几何意义，考查了极坐标方程化普通方程，属于中档题.‎ ‎[选修4-5：不等式选讲] ‎ ‎23.设函数．‎ ‎（1）当时，求函数的定义域；‎ ‎（2）设，当时，成立，求 的取值范围．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用零点分段法解不等式可得出函数的定义域；‎ ‎（2）由可得可得出，然后解不等式可得出，根据题意得出，进而可得出关于实数的不等式组，由此可解得实数的取值范围.‎ ‎【详解】（1）当时，要使函数有意义，需满足.‎ 当时，则有，即，解得，此时；‎ 当时，则有，即，不合乎题意；‎ 当时，则有，即，解得，此时.‎ 综上所述，不等式的解集为.‎ 因此，当时，函数的定义域为；‎ ‎（2）当时，由可得，则，可得，‎ 由可得，解得，‎ ‎，，解得.‎ 因此，实数的取值范围是.‎ ‎【点睛】本题考查含绝对值不等式的求解，同时也考查了含绝对值不等式中参数的求解，第（2）问中将问题转化两区间的包含关系是解答的关键，考查化归与转化思想的应用，属于中等题.‎